7.3 Construction
(matrix [[expr ...+] ...+] maybe-type-ann)
|
| |
| maybe-type-ann | | = | | | | | | | | | : type |
|
Like the
array form for creating arrays, but does not require
#[...] to delimit
nested rows, and the result is constrained to be a
matrix?.
Examples: |
| > (matrix [[1 2 3] [4 5 6]]) | - : (Array Positive-Byte) | (array #[#[1 2 3] #[4 5 6]]) | | > (matrix [[1 2 3] [4 5 6]] : Number) | - : (Array Number) | (array #[#[1 2 3] #[4 5 6]]) | | > (matrix [[]]) | eval:20:0: matrix: given empty row | at: () | in: (matrix (())) |
|
(row-matrix [expr ...+] maybe-type-ann)
|
| |
| maybe-type-ann | | = | | | | | | | | | : type |
|
Examples: |
| > (row-matrix [1 2 3]) | - : (Array Positive-Byte) | (array #[#[1 2 3]]) | | > (row-matrix [1 2 3] : Number) | - : (Array Number) | (array #[#[1 2 3]]) | | > (row-matrix []) | eval:23:0: row-matrix: given empty row | at: () | in: (row-matrix ()) |
|
(col-matrix [expr ...+] maybe-type-ann)
|
| |
| maybe-type-ann | | = | | | | | | | | | : type |
|
Examples: |
| > (col-matrix [1 2 3]) | - : (Array Positive-Byte) | (array #[#[1] #[2] #[3]]) | | > (col-matrix [1 2 3] : Number) | - : (Array Number) | (array #[#[1] #[2] #[3]]) | | > (col-matrix []) | eval:26:0: col-matrix: given empty column | at: () | in: (col-matrix ()) |
|
Returns an n×n identity matrix, which has the value one on the diagonal
and zero everywhere else. The height/width n must be positive.
Examples: |
| > (identity-matrix 3) | - : (Array (U Zero One)) | (array #[#[1 0 0] #[0 1 0] #[0 0 1]]) | | > (identity-matrix 4 1.0+0.0i 0.0+0.0i) | - : (Array Float-Complex) | (array | #[#[1.0+0.0i 0.0+0.0i 0.0+0.0i 0.0+0.0i] | #[0.0+0.0i 1.0+0.0i 0.0+0.0i 0.0+0.0i] | #[0.0+0.0i 0.0+0.0i 1.0+0.0i 0.0+0.0i] | #[0.0+0.0i 0.0+0.0i 0.0+0.0i 1.0+0.0i]]) |
|
|
Returns an
m×
n matrix filled with the value
x;
both
m and
n must be positive.
Analogous to
make-array (and defined in terms of it).
Returns an
m×
n matrix with entries returned by
proc;
both
m and
n must be positive.
Analogous to
build-array (and defined in terms of it).
Returns a matrix with xs along the diagonal and zero everywhere else.
The length of xs must be positive.
Examples: |
| > (diagonal-matrix '(1 2 3 4 5 6)) | - : (Array Byte) | (array | #[#[1 0 0 0 0 0] | #[0 2 0 0 0 0] | #[0 0 3 0 0 0] | #[0 0 0 4 0 0] | #[0 0 0 0 5 0] | #[0 0 0 0 0 6]]) |
| | > (diagonal-matrix '(1.0 2.0 3.0 4.0 5.0) 0.0) | - : (Array (U Positive-Flonum Flonum-Positive-Zero)) | (array | #[#[1.0 0.0 0.0 0.0 0.0] | #[0.0 2.0 0.0 0.0 0.0] | #[0.0 0.0 3.0 0.0 0.0] | #[0.0 0.0 0.0 4.0 0.0] | #[0.0 0.0 0.0 0.0 5.0]]) |
|
|
Examples: |
| - : (Array Byte) | (array | #[#[6 7 0 0 0 0 0 0 0] | #[8 9 0 0 0 0 0 0 0] | #[0 0 7 0 0 0 0 0 0] | #[0 0 0 5 0 0 0 0 0] | #[0 0 0 0 7 0 0 0 0] | #[0 0 0 0 0 1 0 0 0] | #[0 0 0 0 0 2 0 0 0] | #[0 0 0 0 0 3 0 0 0] | #[0 0 0 0 0 0 4 5 6]]) |
| | - : (Array Float-Complex) | (array | #[#[2.0+3.0i 2.0+3.0i 0.0+0.0i 0.0+0.0i] | #[2.0+3.0i 2.0+3.0i 0.0+0.0i 0.0+0.0i] | #[0.0+0.0i 0.0+0.0i 5.0+7.0i 5.0+7.0i] | #[0.0+0.0i 0.0+0.0i 5.0+7.0i 5.0+7.0i]]) |
|
|
Examples: |
| > (vandermonde-matrix '(1 2 3 4) 5) | - : (Array Real) | (array #[#[1 1 1 1 1] #[1 2 4 8 16] #[1 3 9 27 81] #[1 4 16 64 256]]) | | > (vandermonde-matrix '(5.2 3.4 2.0) 3) | - : (Array Flonum) | (array | #[#[1.0 5.2 27.040000000000003] | #[1.0 3.4 11.559999999999999] | #[1.0 2.0 4.0]]) |
|
|
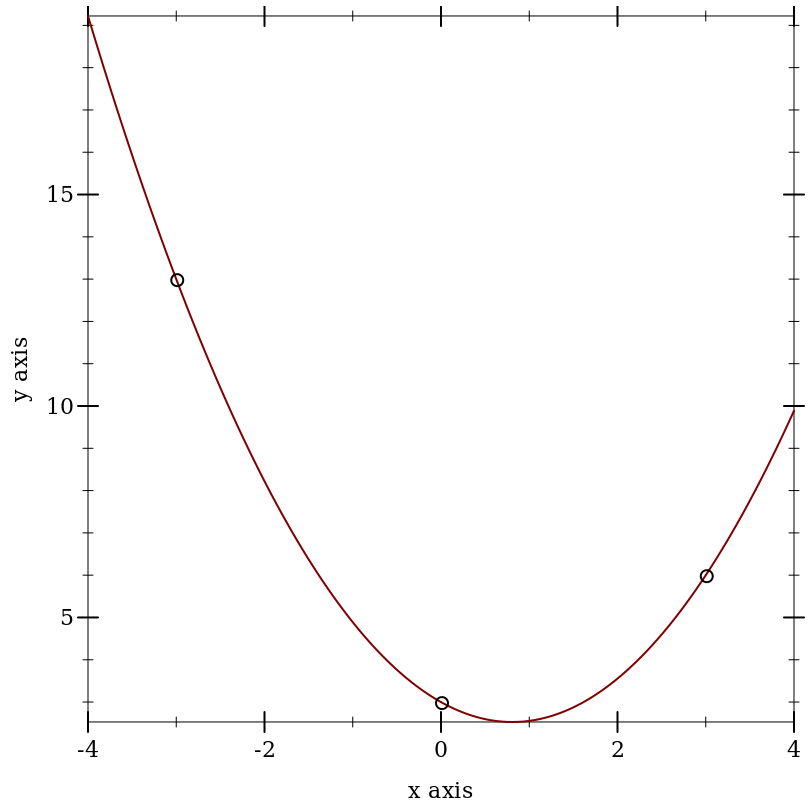
Using a Vandermonde matrix to find a Lagrange polynomial (the polynomial of least degree that passes
through a given set of points):
Note that the above example is in untyped Racket.
This function is defined in terms of array-axis-expand.
| (for/matrix: m n maybe-fill (for:-clause ...) maybe-type-ann | | body ...+) |
|
|
| (for*/matrix: m n maybe-fill (for:-clause ...) maybe-type-ann | | body ...+) |
| | | | maybe-fill | | = | | | | | | | | | #:fill fill | | | | | | | | maybe-type-ann | | = | | | | | | | | | : body-type |
| | | |
|
Like
for/array: and
for*/array:, but for matrices.
The only material difference is that the shape
m n is required and must be positive.
| (for/matrix m n maybe-fill (for-clause ...) | | body ...+) |
|
|
| (for*/matrix m n maybe-fill (for-clause ...) | | body ...+) |
|
|
Untyped versions of the loop macros.