7 Plot Utilities

6.10

7 Plot Utilities

package: plot-lib

7.1 Formatting

procedure
(digits-for-range x-min
x-max
[ base
extra-digits]) → exact-integer?
  x-min : real?
  x-max : real?
  base : (and/c exact-integer? (>=/c 2)) = 10
  extra-digits : exact-integer? = 3

Given a range, returns the number of decimal places necessary to distinguish numbers in the range. This may return negative numbers for large ranges.

Examples:

> (digits-for-range 0.01 0.02)
5
> (digits-for-range 0 100000)
-2

procedure
(real->plot-label x digits [scientific?]) → string?
  x : real?
  digits : exact-integer?
  scientific? : boolean? = #t

Converts a real number to a plot label. Used to format axis tick labels, point-labels, and numbers in legend entries.

Examples:

> (let ([d (digits-for-range 0.01 0.03)])
(real->plot-label 0.02555555 d))
".02556"
> (real->plot-label 2352343 -2)
"2352300"
> (real->plot-label 1000000000.0 4)
"1×10⁹"
> (real->plot-label 1000000000.1234 4)
"(1×10⁹)+.1234"

procedure
(ivl->plot-label i [extra-digits]) → string?
i : ivl?
extra-digits : exact-integer? = 3

Converts an interval to a plot label.

If i = (ivl x-min x-max), the number of digits used is (digits-for-range x-min x-max 10 extra-digits) when both endpoints are rational?. Otherwise, it is unspecified—but will probably remain 15.

Examples:

> (ivl->plot-label (ivl -10.52312 10.99232))
"[-10.52,10.99]"
> (ivl->plot-label (ivl -inf.0 pi))
"[-inf.0,3.141592653589793]"

procedure
(->plot-label a [digits]) → string?
a : any/c
digits : exact-integer? = 7

Converts a Racket value to a label. Used by discrete-histogram and discrete-histogram3d.

procedure
(real->string/trunc x e) → string?
x : real?
e : exact-integer?

Like real->decimal-string, but removes any trailing zeros and any trailing decimal point.

procedure
(real->decimal-string* x
min-digits
[ max-digits]) → string?
  x : real?
  min-digits : exact-nonnegative-integer?
  max-digits : exact-nonnegative-integer? = min-digits

Like real->decimal-string, but accepts both a maximum and minimum number of digits.

Examples:

> (real->decimal-string* 1 5 10)
"1.00000"
> (real->decimal-string* 1.123456 5 10)
"1.123456"
> (real->decimal-string* 1.123456789123456 5 10)
"1.1234567891"

Applying (real->decimal-string* x min-digits) yields the same value as (real->decimal-string x min-digits).

procedure
(integer->superscript x) → string?
x : exact-integer?

Converts an integer into a string of superscript Unicode characters.

Example:

> (integer->superscript -1234567890)
"⁻¹²³⁴⁵⁶⁷⁸⁹⁰"

Systems running some out-of-date versions of Windows XP have difficulty with Unicode superscripts for 4 and up. Because integer->superscript is used by every number formatting function to format exponents, if you have such a system, Plot will apparently not format all numbers with exponents correctly (until you update it).

7.2 Sampling

procedure
(linear-seq start
end
num
[ #:start? start?
#:end? end?]) → (listof real?)
  start : real?
  end : real?
  num : exact-nonnegative-integer?
  start? : boolean? = #t
  end? : boolean? = #t

Returns a list of uniformly spaced real numbers between start and end. If start? is #t, the list includes start. If end? is #t, the list includes end.

This function is used internally to generate sample points.

Examples:

> (linear-seq 0 1 5)
'(0 1/4 1/2 3/4 1)
> (linear-seq 0 1 5 #:start? #f)
'(1/9 1/3 5/9 7/9 1)
> (linear-seq 0 1 5 #:end? #f)
'(0 2/9 4/9 2/3 8/9)
> (linear-seq 0 1 5 #:start? #f #:end? #f)
'(1/10 3/10 1/2 7/10 9/10)
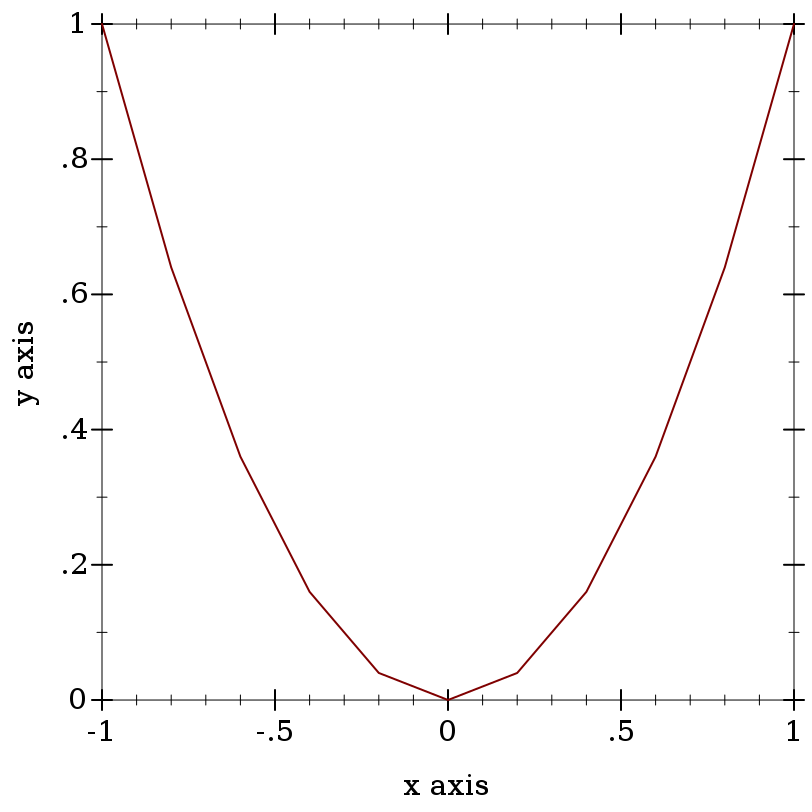
> (define xs (linear-seq -1 1 11))
> (plot (lines (map vector xs (map sqr xs))))

procedure
(linear-seq* points
num
[ #:start? start?
#:end? end?]) → (listof real?)
  points : (listof real?)
  num : exact-nonnegative-integer?
  start? : boolean? = #t
  end? : boolean? = #t

Like linear-seq, but accepts a list of reals instead of a start and end. The #:start? and #:end? keyword arguments work as in linear-seq. This function does not guarantee that each inner value will be in the returned list.

Examples:

> (linear-seq* '(0 1 2) 5)
'(0 1/2 1 3/2 2)
> (linear-seq* '(0 1 2) 6)
'(0 2/5 4/5 6/5 8/5 2)
> (linear-seq* '(0 1 0) 5)
'(0 1/2 1 1/2 0)

procedure
(nonlinear-seq start
end
num
transform
[ #:start? start?
#:end? end?]) → (listof real?)
  start : real?
  end : real?
  num : exact-nonnegative-integer?
  transform : axis-transform/c
  start? : boolean? = #t
  end? : boolean? = #t

Generates a list of reals that, if transformed using transform, would be uniformly spaced. This is used to generate samples for transformed axes.

Examples:

> (linear-seq 1 10 4)
'(1 4 7 10)
> (nonlinear-seq 1 10 4 log-transform)
'(1.0 2.154434690031884 4.641588833612779 10.000000000000002)
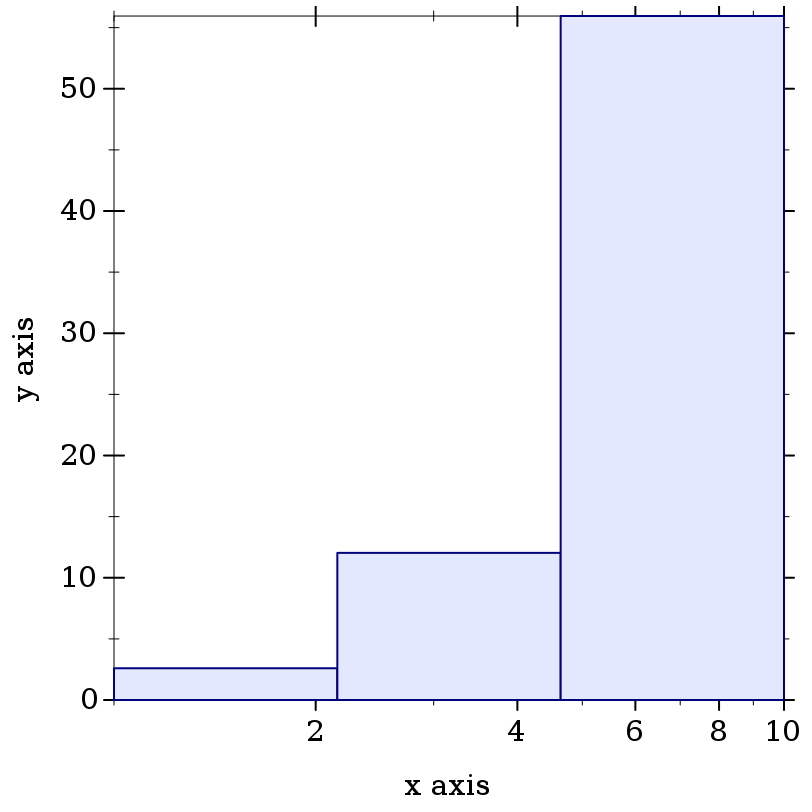
> (parameterize ([plot-x-transform log-transform])
(plot (area-histogram sqr (nonlinear-seq 1 10 4 log-transform))))

procedure
(kde xs h [ws]) →
(-> real? real?)
(or/c rational? #f)
(or/c rational? #f)
  xs : (listof real?)
  h : (>/c 0)
  ws : (or/c (listof (>=/c 0)) #f) = #f

Given optionally weighted samples and a kernel bandwidth, returns a function representing a kernel density estimate, and bounds, outside of which the density estimate is zero. Used by density.

7.3 Plot Colors and Styles

procedure
(color-seq c1
c2
num
[ #:start? start?
#:end? end?])
→ (listof (list/c real? real? real?))
  c1 : color/c
  c2 : color/c
  num : exact-nonnegative-integer?
  start? : boolean? = #t
  end? : boolean? = #t

Interpolates between colors—red, green and blue components separately—using linear-seq. The #:start? and #:end? keyword arguments work as in linear-seq.

Example:

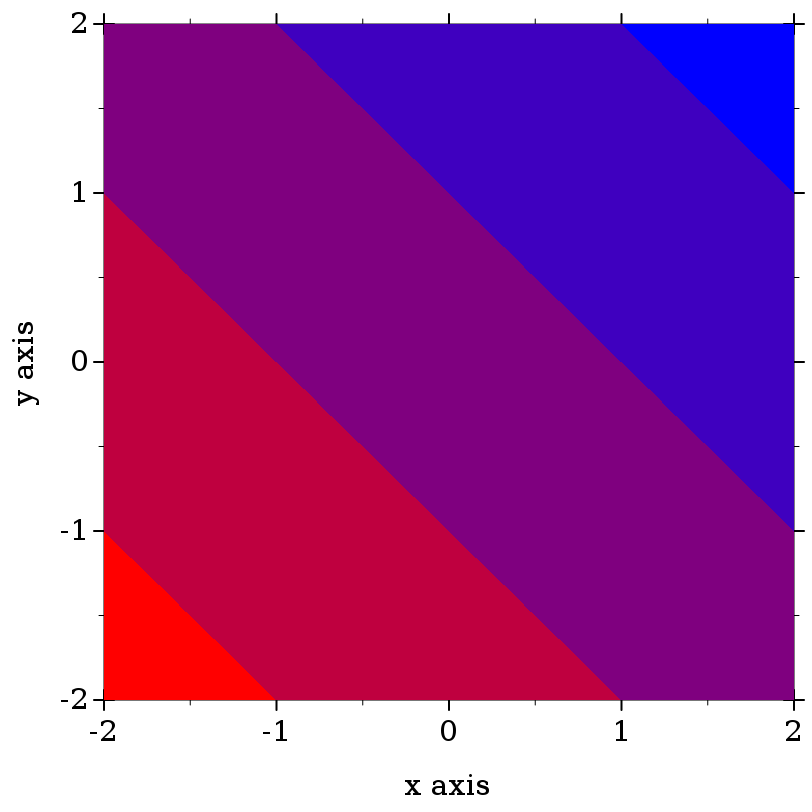
> (plot (contour-intervals (λ (x y) (+ x y)) -2 2 -2 2
#:levels 4 #:contour-styles '(transparent)
#:colors (color-seq "red" "blue" 5)))

procedure
(color-seq* colors
num
[ #:start? start?
#:end? end?])
→ (listof (list/c real? real? real?))
  colors : (listof color/c)
  num : exact-nonnegative-integer?
  start? : boolean? = #t
  end? : boolean? = #t

Interpolates between colors—red, green and blue components separately—using linear-seq*. The #:start? and #:end? keyword arguments work as in linear-seq.

Example:

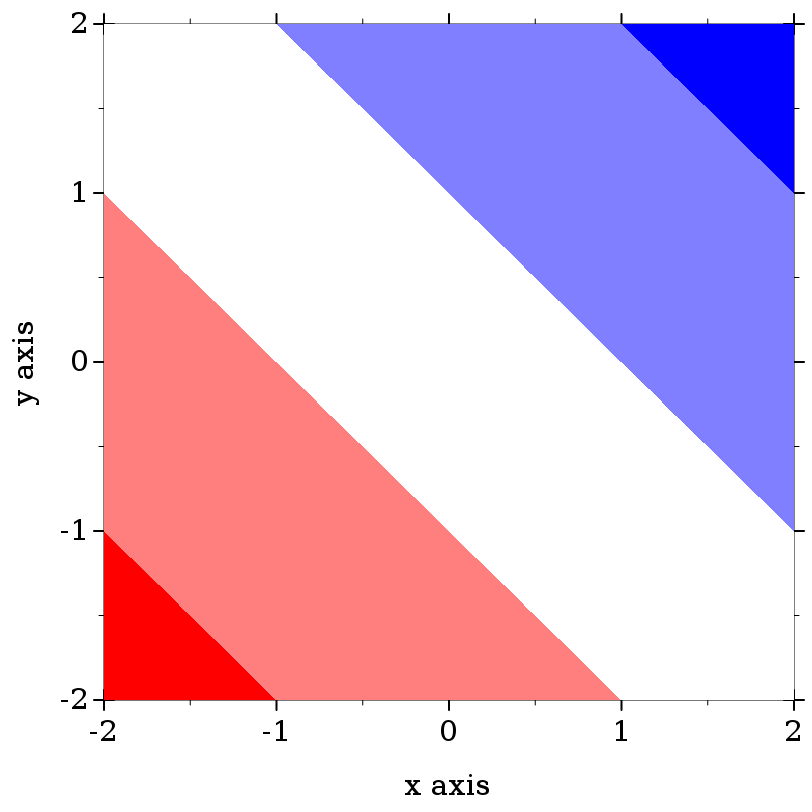
> (plot (contour-intervals (λ (x y) (+ x y)) -2 2 -2 2
#:levels 4 #:contour-styles '(transparent)
#:colors (color-seq* '(red white blue) 5)))

procedure
(->color c) → (list/c real? real? real?)
c : color/c

Converts a non-integer plot color to an RGB triplet.

Symbols are converted to strings, and strings are looked up in a color-database<%>. Lists are unchanged, and color% objects are converted straightforwardly.

Examples:

> (->color 'navy)
'(36 36 140)
> (->color "navy")
'(36 36 140)
> (->color '(36 36 140))
'(36 36 140)
> (->color (make-object color% 36 36 140))
'(36 36 140)

This function does not convert integers to RGB triplets, because there is no way for it to know whether the color will be used for a pen or for a brush. Use ->pen-color and ->brush-color to convert integers.

procedure
(->pen-color c) → (list/c real? real? real?)
c : plot-color/c

Converts a line color to an RGB triplet. This function interprets integer colors as darker and more saturated than ->brush-color does.

Non-integer colors are converted using ->color. Integer colors are chosen for good pairwise contrast, especially between neighbors. Integer colors repeat starting with 128.

Examples:

> (equal? (->pen-color 0) (->pen-color 8))
#f
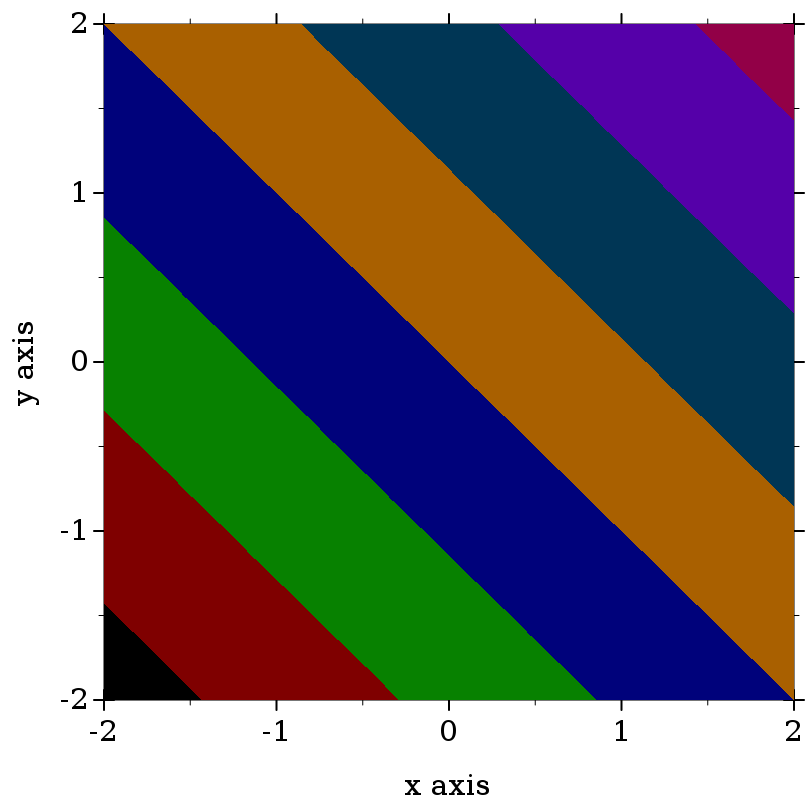
> (plot (contour-intervals
         (λ (x y) (+ x y)) -2 2 -2 2
         #:levels 7 #:contour-styles '(transparent)
         #:colors (map ->pen-color (build-list 8 values))))

procedure
(->brush-color c) → (list/c real? real? real?)
c : plot-color/c

Converts a fill color to an RGB triplet. This function interprets integer colors as lighter and less saturated than ->pen-color does.

Non-integer colors are converted using ->color. Integer colors are chosen for good pairwise contrast, especially between neighbors. Integer colors repeat starting with 128.

Examples:

> (equal? (->brush-color 0) (->brush-color 8))
#f
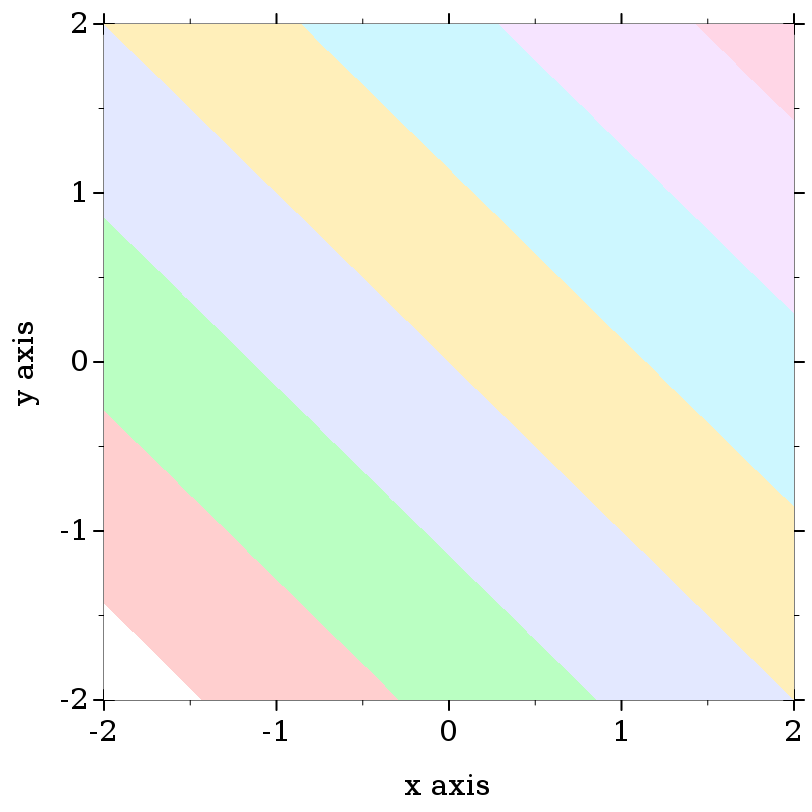
> (plot (contour-intervals
         (λ (x y) (+ x y)) -2 2 -2 2
         #:levels 7 #:contour-styles '(transparent)
         #:colors (map ->brush-color (build-list 8 values))))

In the above example, mapping ->brush-color over the list is actually unnecessary, because contour-intervals uses ->brush-color internally to convert fill colors.

The function-interval function generally plots areas using a fill color and lines using a line color. Both kinds of color have the default value 3. The following example reverses the default behavior; i.e it draws areas using line color 3 and lines using fill color 3:

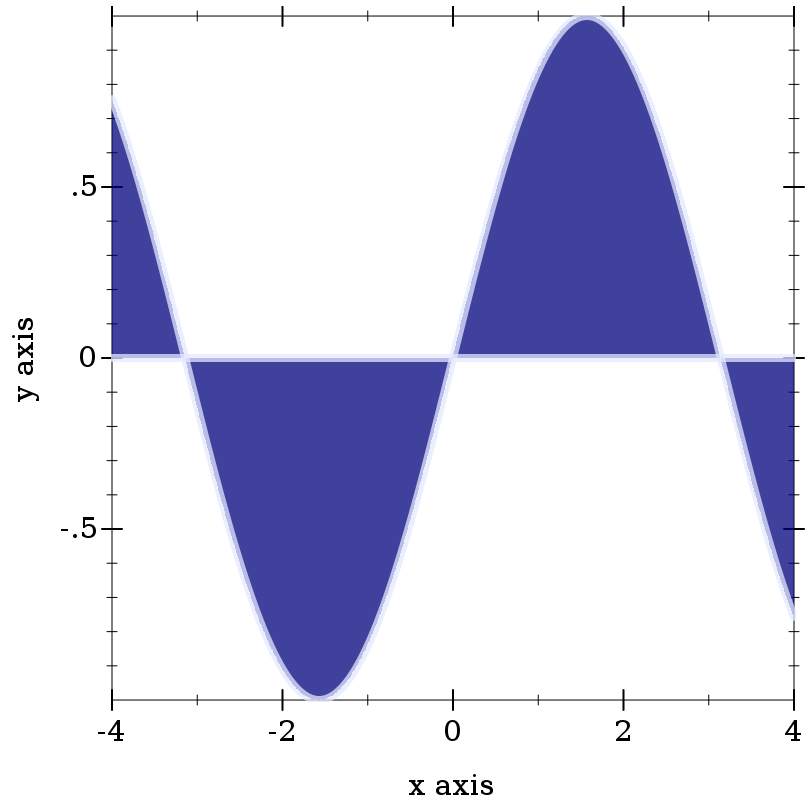
> (plot (function-interval sin (λ (x) 0) -4 4
                           #:color (->pen-color 3)
                           #:line1-color (->brush-color 3)
                           #:line2-color (->brush-color 3)
                           #:line1-width 4 #:line2-width 4))

procedure
(->pen-style s) → symbol?
s : plot-pen-style/c

Converts a symbolic pen style or a number to a symbolic pen style. Symbols are unchanged. Integer pen styles repeat starting at 5.

Examples:

> (eq? (->pen-style 0) (->pen-style 5))
#t
> (map ->pen-style '(0 1 2 3 4))
'(solid dot long-dash short-dash dot-dash)

procedure
(->brush-style s) → symbol?
s : plot-brush-style/c

Converts a symbolic brush style or a number to a symbolic brush style. Symbols are unchanged. Integer brush styles repeat starting at 7.

Examples:

> (eq? (->brush-style 0) (->brush-style 7))
#t
> (map ->brush-style '(0 1 2 3))
'(solid bdiagonal-hatch fdiagonal-hatch crossdiag-hatch)
> (map ->brush-style '(4 5 6))
'(horizontal-hatch vertical-hatch cross-hatch)

7.4 Plot-Specific Math

7.4.1 Real Functions

procedure
(polar->cartesian θ r) → (vector/c real? real?)
θ : real?
r : real?

Converts 2D polar coordinates to 3D cartesian coordinates.

procedure
(3d-polar->3d-cartesian θ ρ r) → (vector/c real? real? real?)
  θ : real?
  ρ : real?
  r : real?

Converts 3D polar coordinates to 3D cartesian coordinates. See parametric3d for an example of use.

procedure
(ceiling-log/base b x) → exact-integer?
b : (and/c exact-integer? (>=/c 2))
x : (>/c 0)

Like (ceiling (/ (log x) (log b))), but ceiling-log/base is not susceptible to floating-point error.

Examples:

> (ceiling (/ (log 100) (log 10)))
2.0
> (ceiling-log/base 10 100)
2
> (ceiling (/ (log 1/1000) (log 10)))
-2.0
> (ceiling-log/base 10 1/1000)
-3

Various number-formatting functions use this.

procedure
(floor-log/base b x) → exact-integer?
b : (and/c exact-integer? (>=/c 2))
x : (>/c 0)

Like (floor (/ (log x) (log b))), but floor-log/base is not susceptible to floating-point error.

Examples:

> (floor (/ (log 100) (log 10)))
2.0
> (floor-log/base 10 100)
2
> (floor (/ (log 1000) (log 10)))
2.0
> (floor-log/base 10 1000)
3

This is a generalization of order-of-magnitude.

procedure
(maybe-inexact->exact x) → (or/c rational? #f)
x : (or/c rational? #f)

Returns #f if x is #f; otherwise (inexact->exact x). Use this to convert interval endpoints, which may be #f, to exact numbers.

7.4.2 Vector Functions

procedure
(v+ v1 v2) → (vectorof real?)
  v1 : (vectorof real?)
  v2 : (vectorof real?)
procedure
(v- v1 v2) → (vectorof real?)
  v1 : (vectorof real?)
  v2 : (vectorof real?)
procedure
(vneg v) → (vectorof real?)
  v : (vectorof real?)
procedure
(v* v c) → (vectorof real?)
  v : (vectorof real?)
  c : real?
procedure
(v/ v c) → (vectorof real?)
  v : (vectorof real?)
  c : real?

Vector arithmetic. Equivalent to vector-mapp-ing arithmetic operators over vectors, but specialized so that 2- and 3-vector operations are much faster.

Examples:

> (v+ #(1 2) #(3 4))
'#(4 6)
> (v- #(1 2) #(3 4))
'#(-2 -2)
> (vneg #(1 2))
'#(-1 -2)
> (v* #(1 2 3) 2)
'#(2 4 6)
> (v/ #(1 2 3) 2)
'#(1/2 1 3/2)

procedure
(v= v1 v2) → boolean?
v1 : (vectorof real?)
v2 : (vectorof real?)

Like equal? specialized to numeric vectors, but compares elements using =.

Examples:

> (equal? #(1 2) #(1 2))
#t
> (equal? #(1 2) #(1.0 2.0))
#f
> (v= #(1 2) #(1.0 2.0))
#t

procedure
(vcross v1 v2) → (vector/c real? real? real?)
v1 : (vector/c real? real? real?)
v2 : (vector/c real? real? real?)

Returns the right-hand vector cross product of v1 and v2.

Examples:

> (vcross #(1 0 0) #(0 1 0))
'#(0 0 1)
> (vcross #(0 1 0) #(1 0 0))
'#(0 0 -1)
> (vcross #(0 0 1) #(0 0 1))
'#(0 0 0)

procedure
(vcross2 v1 v2) → real?
v1 : (vector/c real? real?)
v2 : (vector/c real? real?)

Returns the signed area of the 2D parallelogram with sides v1 and v2. Equivalent to (vector-ref (vcross (vector-append v1 #(0)) (vector-append v2 #(0))) 2) but faster.

Examples:

> (vcross2 #(1 0) #(0 1))
1
> (vcross2 #(0 1) #(1 0))
-1

procedure
(vdot v1 v2) → real?
v1 : (vectorof real?)
v2 : (vectorof real?)

Returns the dot product of v1 and v2.

procedure
(vmag^2 v) → real?
v : (vectorof real?)

Returns the squared magnitude of v. Equivalent to (vdot v v).

procedure
(vmag v) → real?
v : (vectorof real?)

Returns the magnitude of v. Equivalent to (sqrt (vmag^2 v)).

procedure
(vnormalize v) → (vectorof real?)
v : (vectorof real?)

Returns a normal vector in the same direction as v. If v is a zero vector, returns v.

Examples:

> (vnormalize #(1 1 0))
'#(0.7071067811865475 0.7071067811865475 0)
> (vnormalize #(1 1 1))
'#(0.5773502691896258 0.5773502691896258 0.5773502691896258)
> (vnormalize #(0 0 0.0))
'#(0 0 0.0)

procedure
(vcenter vs) → (vectorof real?)
vs : (listof (vectorof real?))

Returns the center of the smallest bounding box that contains vs.

Example:

> (vcenter '(#(1 1) #(2 2)))
'#(3/2 3/2)

procedure
(vrational? v) → boolean?
v : (vectorof real?)

Returns #t if every element of v is rational?.

Examples:

> (vrational? #(1 2))
#t
> (vrational? #(+inf.0 2))
#f
> (vrational? #(#f 1))
vrational?: contract violation
  expected: Real
  given: #f
  in: an element of
      the 1st argument of
      (-> (vectorof Real) any)
  contract from:
      <pkgs>/plot-lib/plot/private/common/math.rkt
  blaming: top-level
   (assuming the contract is correct)
  at: <pkgs>/plot-lib/plot/private/common/math.rkt:330.9

7.4.3 Intervals and Interval Functions

struct
(struct ivl (min max)
    #:extra-constructor-name make-ivl)
  min : real?
  max : real?

Represents a closed interval.

An interval with two real-valued endpoints always contains the endpoints in order:

> (ivl 0 1)
(ivl 0 1)
> (ivl 1 0)
(ivl 0 1)

An interval can have infinite endpoints:

> (ivl -inf.0 0)
(ivl -inf.0 0)
> (ivl 0 +inf.0)
(ivl 0 +inf.0)
> (ivl -inf.0 +inf.0)
(ivl -inf.0 +inf.0)

Functions that return rectangle renderers, such as rectangles and discrete-histogram3d, accept vectors of ivls as arguments. The ivl struct type is also provided by plot so users of such renderers do not have to require plot/utils.

procedure
(rational-ivl? i) → boolean?
i : any/c

Returns #t if i is an interval and each of its endpoints is rational?.

Example:

> (map rational-ivl? (list (ivl -1 1) (ivl -inf.0 2) 'bob))
'(#t #f #f)

procedure
(bounds->intervals xs) → (listof ivl?)
xs : (listof real?)

Given a list of points, returns intervals between each pair.

Use this to construct inputs for rectangles and rectangles3d.

Example:

> (bounds->intervals (linear-seq 0 1 5))
(list (ivl 0 1/4) (ivl 1/4 1/2) (ivl 1/2 3/4) (ivl 3/4 1))

procedure
(clamp-real x i) → real?
x : real?
i : ivl?

7.5 Dates and Times

procedure
(datetime->real x) → real?
x : (or/c plot-time? date? date*? sql-date? sql-time? sql-timestamp?)

Converts various date/time representations into UTC seconds, respecting time zone offsets.

For dates, the value returned is the number of seconds since a system-dependent UTC epoch. See date-ticks for more information.

To plot a time series using dates pulled from an SQL database, simply set the relevant axis ticks (probably plot-x-ticks) to date-ticks, and convert the dates to seconds using datetime->real before passing them to lines. To keep time zone offsets from influencing the plot, set them to 0 first.

struct
(struct plot-time (second minute hour day)
    #:extra-constructor-name make-plot-time)
  second : (and/c (>=/c 0) (</c 60))
  minute : (integer-in 0 59)
  hour : (integer-in 0 23)
  day : exact-integer?

A time representation that accounts for days, negative times (using negative days), and fractional seconds.

Plot (specifically time-ticks) uses plot-time internally to format times, but because renderer-producing functions require only real values, user code should not need it. It is provided just in case.

procedure
(plot-time->seconds t) → real?
t : plot-time?
procedure
(seconds->plot-time s) → plot-time?
s : real?

Convert plot-times to real seconds, and vice-versa.

Examples:

> (define (plot-time+ t1 t2)
    (seconds->plot-time (+ (plot-time->seconds t1)
                           (plot-time->seconds t2))))
> (plot-time+ (plot-time 32 0 12 1)
              (plot-time 32 0 14 1))
(plot-time 4 1 2 3)

top ← prev up next →

1	Introduction
2	2D and 3D Plotting Procedures
3	2D Renderers
4	3D Renderers
5	Nonrenderers
6	Axis Transforms and Ticks
7	Plot Utilities
8	Plot and Renderer Parameters
9	Plot Contracts
10	Porting From Plot <= 5.1.3
11	Legacy Typed Interface
12	Compatibility Module

7.1	Formatting
7.2	Sampling
7.3	Plot Colors and Styles
7.4	Plot-Specific Math
7.5	Dates and Times