1 Type Reference

6.10

top ← prev up next →

1 Type Reference

syntax
Any

Any Racket value. All other types are subtypes of Any.

syntax
AnyValues

Any number of Racket values of any type.

syntax
Nothing

The empty type. No values inhabit this type, and any expression of this type will not evaluate to a value.

1.1 Base Types

1.1.1 Numeric Types

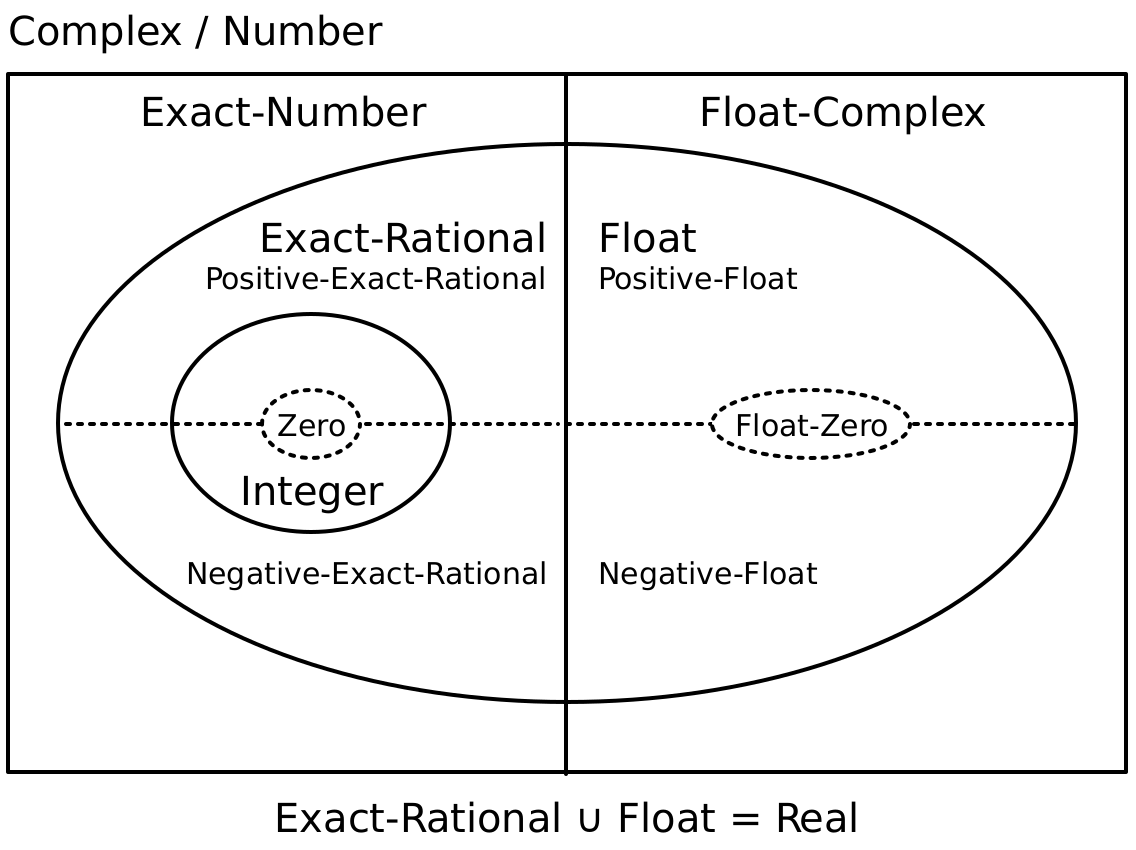
These types represent the hierarchy of numbers of Racket. The diagram below shows the relationships between the types in the hierarchy.

The regions with a solid border are layers of the numeric hierarchy corresponding to sets of numbers such as integers or rationals. Layers contained within another are subtypes of the layer containing them. For example, Exact-Rational is a subtype of Exact-Number.

The Real layer is also divided into positive and negative types (shown with a dotted line). The Integer layer is subdivided into several fixed-width integers types, detailed later in this section.

syntax
Number
syntax
Complex

Number and Complex are synonyms. This is the most general numeric type, including all Racket numbers, both exact and inexact, including complex numbers.

syntax
Integer

Includes Racket’s exact integers and corresponds to the exact-integer? predicate. This is the most general type that is still valid for indexing and other operations that require integral values.

syntax
Float
syntax
Flonum

Includes Racket’s double-precision (default) floating-point numbers and corresponds to the flonum? predicate. This type excludes single-precision floating-point numbers.

syntax
Single-Flonum

Includes Racket’s single-precision floating-point numbers and corresponds to the single-flonum? predicate. This type excludes double-precision floating-point numbers.

syntax
Inexact-Real

Includes all of Racket’s floating-point numbers, both single- and double-precision.

syntax
Exact-Rational

Includes Racket’s exact rationals, which include fractions and exact integers.

syntax
Real

Includes all of Racket’s real numbers, which include both exact rationals and all floating-point numbers. This is the most general type for which comparisons (e.g. <) are defined.

syntax
Exact-Number
syntax
Float-Complex
syntax
Single-Flonum-Complex
syntax
Inexact-Complex

These types correspond to Racket’s complex numbers.

The above types can be subdivided into more precise types if you want to enforce tighter constraints. Typed Racket provides types for the positive, negative, non-negative and non-positive subsets of the above types (where applicable).

syntax
Positive-Integer
syntax
Exact-Positive-Integer
syntax
Nonnegative-Integer
syntax
Exact-Nonnegative-Integer
syntax
Natural
syntax
Negative-Integer
syntax
Nonpositive-Integer
syntax
Zero
syntax
Positive-Float
syntax
Positive-Flonum
syntax
Nonnegative-Float
syntax
Nonnegative-Flonum
syntax
Negative-Float
syntax
Negative-Flonum
syntax
Nonpositive-Float
syntax
Nonpositive-Flonum
syntax
Float-Negative-Zero
syntax
Flonum-Negative-Zero
syntax
Float-Positive-Zero
syntax
Flonum-Positive-Zero
syntax
Float-Zero
syntax
Flonum-Zero
syntax
Float-Nan
syntax
Flonum-Nan
syntax
Positive-Single-Flonum
syntax
Nonnegative-Single-Flonum
syntax
Negative-Single-Flonum
syntax
Nonpositive-Single-Flonum
syntax
Single-Flonum-Negative-Zero
syntax
Single-Flonum-Positive-Zero
syntax
Single-Flonum-Zero
syntax
Single-Flonum-Nan
syntax
Positive-Inexact-Real
syntax
Nonnegative-Inexact-Real
syntax
Negative-Inexact-Real
syntax
Nonpositive-Inexact-Real
syntax
Inexact-Real-Negative-Zero
syntax
Inexact-Real-Positive-Zero
syntax
Inexact-Real-Zero
syntax
Inexact-Real-Nan
syntax
Positive-Exact-Rational
syntax
Nonnegative-Exact-Rational
syntax
Negative-Exact-Rational
syntax
Nonpositive-Exact-Rational
syntax
Positive-Real
syntax
Nonnegative-Real
syntax
Negative-Real
syntax
Nonpositive-Real
syntax
Real-Zero

Natural and Exact-Nonnegative-Integer are synonyms. So are the integer and exact-integer types, and the float and flonum types. Zero includes only the integer 0. Real-Zero includes exact 0 and all the floating-point zeroes.

These types are useful when enforcing that values have a specific sign. However, programs using them may require additional dynamic checks when the type-checker cannot guarantee that the sign constraints will be respected.

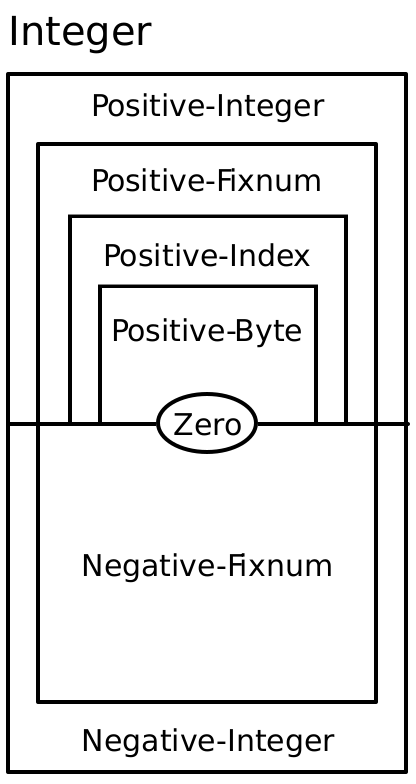
In addition to being divided by sign, integers are further subdivided into range-bounded types. The relationships between most of the range-bounded types are shown in this diagram:

Like the previous diagram, types nested inside of another in the diagram are subtypes of its containing types.

syntax
One
syntax
Byte
syntax
Positive-Byte
syntax
Index
syntax
Positive-Index
syntax
Fixnum
syntax
Positive-Fixnum
syntax
Nonnegative-Fixnum
syntax
Negative-Fixnum
syntax
Nonpositive-Fixnum

One includes only the integer 1. Byte includes numbers from 0 to 255. Index is bounded by 0 and by the length of the longest possible Racket vector. Fixnum includes all numbers represented by Racket as machine integers. For the latter two families, the sets of values included in the types are architecture-dependent, but typechecking is architecture-independent.

These types are useful to enforce bounds on numeric values, but given the limited amount of closure properties these types offer, dynamic checks may be needed to check the desired bounds at runtime.

Examples:

> 7
- : Integer [more precisely: Positive-Byte]
7
> 8.3
- : Flonum [more precisely: Positive-Flonum]
8.3
> (/ 8 3)
- : Exact-Rational [more precisely: Positive-Exact-Rational]
8/3
> 0
- : Integer [more precisely: Zero]
0
> -12
- : Integer [more precisely: Negative-Fixnum]
-12
> 3+4i
- : Exact-Number
3+4i

syntax
ExtFlonum
syntax
Positive-ExtFlonum
syntax
Nonnegative-ExtFlonum
syntax
Negative-ExtFlonum
syntax
Nonpositive-ExtFlonum
syntax
ExtFlonum-Negative-Zero
syntax
ExtFlonum-Positive-Zero
syntax
ExtFlonum-Zero
syntax
ExtFlonum-Nan

80-bit extflonum types, for the values operated on by racket/extflonum exports. These are not part of the numeric tower.

1.1.2 Other Base Types

syntax
Boolean
syntax
True
syntax
False
syntax
String
syntax
Keyword
syntax
Symbol
syntax
Char
syntax
Void
syntax
Input-Port
syntax
Output-Port
syntax
Port
syntax
Path
syntax
Path-For-Some-System
syntax
Regexp
syntax
PRegexp
syntax
Byte-Regexp
syntax
Byte-PRegexp
syntax
Bytes
syntax
Namespace
syntax
Namespace-Anchor
syntax
Variable-Reference
syntax
Null
syntax
EOF
syntax
Continuation-Mark-Set
syntax
Undefined
syntax
Module-Path
syntax
Module-Path-Index
syntax
Resolved-Module-Path
syntax
Compiled-Module-Expression
syntax
Compiled-Expression
syntax
Internal-Definition-Context
syntax
Pretty-Print-Style-Table
syntax
Special-Comment
syntax
Struct-Type-Property
syntax
Impersonator-Property
syntax
Read-Table
syntax
Bytes-Converter
syntax
Parameterization
syntax
Custodian
syntax
Inspector
syntax
Security-Guard
syntax
UDP-Socket
syntax
TCP-Listener
syntax
Logger
syntax
Log-Receiver
syntax
Log-Level
syntax
Thread
syntax
Thread-Group
syntax
Subprocess
syntax
Place
syntax
Place-Channel
syntax
Semaphore
syntax
FSemaphore
syntax
Will-Executor
syntax
Pseudo-Random-Generator
syntax
Environment-Variables

These types represent primitive Racket data.

Examples:

> #t
- : Boolean [more precisely: True]
#t
> #f
- : False
#f
> "hello"
- : String
"hello"
> (current-input-port)
- : Input-Port
#<input-port:string>
> (current-output-port)
- : Output-Port
#<output-port:string>
> (string->path "/")
- : Path
#<path:/>
> #rx"a*b*"
- : Regexp
#rx"a*b*"
> #px"a*b*"
- : PRegexp
#px"a*b*"
> '#"bytes"
- : Bytes
#"bytes"
> (current-namespace)
- : Namespace
#<namespace:0>
> #\b
- : Char
#\b
> (thread (lambda () (add1 7)))
- : Thread
#<thread>

syntax
Path-String

The union of the Path and String types. Note that this does not match exactly what the predicate path-string? recognizes. For example, strings that contain the character #\nul have the type Path-String but path-string? returns #f for those strings. For a complete specification of which strings path-string? accepts, see its documentation.

1.2 Singleton Types

Some kinds of data are given singleton types by default. In particular, booleans, symbols, and keywords have types which consist only of the particular boolean, symbol, or keyword. These types are subtypes of Boolean, Symbol and Keyword, respectively.

Examples:

> #t
- : Boolean [more precisely: True]
#t
> '#:foo
- : '#:foo
'#:foo
> 'bar
- : Symbol [more precisely: 'bar]
'bar

1.3 Containers

The following base types are parametric in their type arguments.

syntax
(Pairof s t)

is the pair containing s as the car and t as the cdr

Examples:

> (cons 1 2)
- : (Pairof One Positive-Byte)
'(1 . 2)
> (cons 1 "one")
- : (Pairof One String)
'(1 . "one")

syntax
(Listof t)

Homogenous lists of t

syntax
(List t ...)

is the type of the list with one element, in order, for each type provided to the List type constructor.

syntax
(List t ... trest ... bound)

is the type of a list with one element for each of the ts, plus a sequence of elements corresponding to trest, where bound must be an identifier denoting a type variable bound with ....

syntax
(List* t t1 ... s)

is equivalent to (Pairof t (List* t1 ... s)).

Examples:

> (list 'a 'b 'c)
- : (Listof (U 'a 'b 'c)) [more precisely: (List 'a 'b 'c)]
'(a b c)
> (plambda: (a ...) ([sym : Symbol] boxes : (Boxof a) ... a)
(ann (cons sym boxes) (List Symbol (Boxof a) ... a)))
- : (All (a ...)
(-> Symbol (Boxof a) ... a (Pairof Symbol (List (Boxof a) ... a))))
#<procedure>
> (map symbol->string (list 'a 'b 'c))
- : (Listof String) [more precisely: (Pairof String (Listof String))]
'("a" "b" "c")

syntax
(MListof t)

Homogenous mutable lists of t.

syntax
(MPairof t u)

Mutable pairs of t and u.

syntax
MPairTop

is the type of a mutable pair with unknown element types and is the supertype of all mutable pair types. This type typically appears in programs via the combination of occurrence typing and mpair?.

Example:

> (lambda: ([x : Any]) (if (mpair? x) x (error "not an mpair!")))
- : (-> Any MPairTop)
#<procedure>

syntax
(Boxof t)

A box of t

Example:

> (box "hello world")
- : (Boxof String)
'#&"hello world"

syntax
BoxTop

is the type of a box with an unknown element type and is the supertype of all box types. Only read-only box operations (e.g. unbox) are allowed on values of this type. This type typically appears in programs via the combination of occurrence typing and box?.

Example:

> (lambda: ([x : Any]) (if (box? x) x (error "not a box!")))
- : (-> Any BoxTop)
#<procedure>

syntax
(Vectorof t)

Homogenous vectors of t

syntax
(Vector t ...)

is the type of the vector with one element, in order, for each type provided to the Vector type constructor.

Examples:

> (vector 1 2 3)
- : (Vector Integer Integer Integer)
'#(1 2 3)
> #(a b c)
- : (Vector Symbol Symbol Symbol)
'#(a b c)

syntax
FlVector

An flvector.

Example:

> (flvector 1.0 2.0 3.0)
- : FlVector
(flvector 1.0 2.0 3.0)

syntax
ExtFlVector

An extflvector.

Example:

> (extflvector 1.0t0 2.0t0 3.0t0)
- : ExtFlVector
#<extflvector>

syntax
FxVector

An fxvector.

Example:

> (fxvector 1 2 3)
- : FxVector
(fxvector 1 2 3)

syntax
VectorTop

is the type of a vector with unknown length and element types and is the supertype of all vector types. Only read-only vector operations (e.g. vector-ref) are allowed on values of this type. This type typically appears in programs via the combination of occurrence typing and vector?.

Example:

> (lambda: ([x : Any]) (if (vector? x) x (error "not a vector!")))
- : (-> Any VectorTop)
#<procedure>

syntax
(Immutable-HashTable k v)

is the type of an immutable hash table with key type k and value type v.

Example:

> #hash((a . 1) (b . 2))
- : (U (Immutable-HashTable Symbol Integer)
(Mutable-HashTable Symbol Integer)
(Weak-HashTable Symbol Integer)) [more precisely: (Immutable-HashTable Symbol Integer)]
'#hash((a . 1) (b . 2))

syntax
(Mutable-HashTable k v)

is the type of a mutable hash table that holds keys strongly (see Weak Boxes) with key type k and value type v.

Example:

> (make-hash '((a . 1) (b . 2)))
- : (U (Immutable-HashTable Symbol Integer)
(Mutable-HashTable Symbol Integer)
(Weak-HashTable Symbol Integer)) [more precisely: (Mutable-HashTable Symbol Integer)]
'#hash((b . 2) (a . 1))

syntax
(Weak-HashTable k v)

is the type of a mutable hash table that holds keys weakly with key type k and value type v.

Example:

> (make-weak-hash '((a . 1) (b . 2)))
- : (U (Immutable-HashTable Symbol Integer)
(Mutable-HashTable Symbol Integer)
(Weak-HashTable Symbol Integer)) [more precisely: (Weak-HashTable Symbol Integer)]
'#hash((b . 2) (a . 1))

syntax
(HashTable k v)

is the type of a mutable or immutable hash table with key type k and value type v.

Example:

> (make-hash '((a . 1) (b . 2)))
- : (U (Immutable-HashTable Symbol Integer)
(Mutable-HashTable Symbol Integer)
(Weak-HashTable Symbol Integer)) [more precisely: (Mutable-HashTable Symbol Integer)]
'#hash((b . 2) (a . 1))

syntax
HashTableTop

is the type of a hash table with unknown key and value types and is the supertype of all hash table types. Only read-only hash table operations (e.g. hash-ref) are allowed on values of this type. This type typically appears in programs via the combination of occurrence typing and hash?.

Example:

> (lambda: ([x : Any]) (if (hash? x) x (error "not a hash table!")))
- : (-> Any HashTableTop)
#<procedure>

syntax
Mutable-HashTableTop

is the type of a mutable hash table that holds keys strongly with unknown key and value types.

syntax
Weak-HashTableTop

is the type of a mutable hash table that holds keys weakly with unknown key and value types.

syntax
(Setof t)

is the type of a hash set of t. This includes custom hash sets, but not mutable hash set or sets that are implemented using gen:set.

Example:

> (set 0 1 2 3)
- : (Setof Byte)
(set 1 3 2 0)

Example:

> (seteq 0 1 2 3)
- : (Setof Byte)
(seteq 0 1 2 3)

syntax
(Channelof t)

A channel on which only ts can be sent.

Example:

> (ann (make-channel) (Channelof Symbol))
- : (Channelof Symbol)
#<channel>

syntax
ChannelTop

is the type of a channel with unknown message type and is the supertype of all channel types. This type typically appears in programs via the combination of occurrence typing and channel?.

Example:

> (lambda: ([x : Any]) (if (channel? x) x (error "not a channel!")))
- : (-> Any ChannelTop)
#<procedure>

syntax
(Async-Channelof t)

An asynchronous channel on which only ts can be sent.

Examples:

> (require typed/racket/async-channel)
> (ann (make-async-channel) (Async-Channelof Symbol))
- : (Async-Channelof Symbol)
#<async-channel>

Added in version 1.1 of package typed-racket-lib.

syntax
Async-ChannelTop

is the type of an asynchronous channel with unknown message type and is the supertype of all asynchronous channel types. This type typically appears in programs via the combination of occurrence typing and async-channel?.

Examples:

> (require typed/racket/async-channel)
> (lambda: ([x : Any]) (if (async-channel? x) x (error "not an async-channel!")))
- : (-> Any Async-ChannelTop)
#<procedure>

Added in version 1.1 of package typed-racket-lib.

syntax
(Parameterof t)
(Parameterof s t)

A parameter of t. If two type arguments are supplied, the first is the type the parameter accepts, and the second is the type returned.

Examples:

> current-input-port
- : (Parameterof Input-Port)
#<procedure:current-input-port>
> current-directory
- : (Parameterof Path-String Path)
#<procedure:current-directory>

syntax
(Promise t)

A promise of t.

Example:

> (delay 3)
- : (Promise Positive-Byte)
#<promise:eval:51:0>

syntax
(Futureof t)

A future which produce a value of type t when touched.

syntax
(Sequenceof t)

A sequence that produces values of type t on each iteration.

syntax
(Custodian-Boxof t)

A custodian box of t.

syntax
(Thread-Cellof t)

A thread cell of t.

syntax
Thread-CellTop

is the type of a thread cell with unknown element type and is the supertype of all thread cell types. This type typically appears in programs via the combination of occurrence typing and thread-cell?.

Example:

> (lambda: ([x : Any]) (if (thread-cell? x) x (error "not a thread cell!")))
- : (-> Any Thread-CellTop)
#<procedure>

syntax
(Weak-Boxof t)

The type for a weak box whose value is of type t.

Examples:

> (make-weak-box 5)
- : (Weak-Boxof Integer)
#<weak-box>
> (weak-box-value (make-weak-box 5))
- : (U False Integer)
5

syntax
Weak-BoxTop

is the type of a weak box with an unknown element type and is the supertype of all weak box types. This type typically appears in programs via the combination of occurrence typing and weak-box?.

Example:

> (lambda: ([x : Any]) (if (weak-box? x) x (error "not a box!")))
- : (-> Any Weak-BoxTop)
#<procedure>

syntax
(Ephemeronof t)

An ephemeron whose value is of type t.

syntax
(Evtof t)

A synchronizable event whose synchronization result is of type t.

Examples:

> always-evt
- : (Rec x (Evtof x))
#<always-evt>
> (system-idle-evt)
- : (Evtof Void)
#<evt>
> (ann (thread (λ () (displayln "hello world"))) (Evtof Thread))
- : (Evtof Thread)
#<thread>

1.4 Syntax Objects

The following types represent syntax objects and their content.

syntax
(Syntaxof t)

A syntax object with content of type t. Applying syntax-e to a value of type (Syntaxof t) produces a value of type t.

syntax
Identifier

A syntax object containing a symbol. Equivalent to (Syntaxof Symbol).

syntax
Syntax

A syntax object containing only symbols, keywords, strings, characters, booleans, numbers, boxes containing Syntax, vectors of Syntax, or (possibly improper) lists of Syntax. Equivalent to (Syntaxof Syntax-E).

syntax
Syntax-E

The content of syntax objects of type Syntax. Applying syntax-e to a value of type Syntax produces a value of type Syntax-E.

syntax
(Sexpof t)

The recursive union of t with symbols, keywords, strings, characters, booleans, numbers, boxes, vectors, and (possibly improper) lists.

syntax
Sexp

Applying syntax->datum to a value of type Syntax produces a value of type Sexp. Equivalent to (Sexpof Nothing).

syntax
Datum

Applying datum->syntax to a value of type Datum produces a value of type Syntax. Equivalent to (Sexpof Syntax).

1.5 Control

The following types represent prompt tags and keys for continuation marks for use with delimited continuation functions and continuation mark functions.

syntax
(Prompt-Tagof s t)

A prompt tag to be used in a continuation prompt whose body produces the type s and whose handler has the type t. The type t must be a function type.

The domain of t determines the type of the values that can be aborted, using abort-current-continuation, to a prompt with this prompt tag.

Example:

> (make-continuation-prompt-tag 'prompt-tag)
hello world
- : (Prompt-Tagof Any Any)
#<continuation-prompt-tag:prompt-tag>

syntax
Prompt-TagTop

is the type of a prompt tag with unknown body and handler types and is the supertype of all prompt tag types. This type typically appears in programs via the combination of occurrence typing and continuation-prompt-tag?.

Example:

> (lambda: ([x : Any]) (if (continuation-prompt-tag? x) x (error "not a prompt tag!")))
- : (-> Any Prompt-TagTop)
#<procedure>

syntax
(Continuation-Mark-Keyof t)

A continuation mark key that is used for continuation mark operations such as with-continuation-mark and continuation-mark-set->list. The type t represents the type of the data that is stored in the continuation mark with this key.

Example:

> (make-continuation-mark-key 'mark-key)
- : (Continuation-Mark-Keyof Any)
#<continuation-mark-key>

syntax
Continuation-Mark-KeyTop

is the type of a continuation mark key with unknown element type and is the supertype of all continuation mark key types. This type typically appears in programs via the combination of occurrence typing and continuation-mark-key?.

Example:

> (lambda: ([x : Any]) (if (continuation-mark-key? x) x (error "not a mark key!")))
- : (-> Any Continuation-Mark-KeyTop)
#<procedure>

1.6 Other Type Constructors

syntax
(-> dom ... rng opt-proposition)
(-> dom ... rest * rng)
(-> dom ... rest ooo bound rng)
(dom ... -> rng opt-proposition)
(dom ... rest * -> rng)
(dom ... rest ooo bound -> rng)

ooo = ...

dom = type
| mandatory-kw
| opt-kw

mandatory-kw = keyword type

opt-kw = [keyword type]

opt-proposition =
| : type
|
: pos-proposition
neg-proposition
object

pos-proposition =
| #:+ proposition ...

neg-proposition =
| #:- proposition ...

object =
| #:object index

proposition = Top
| Bot
| type
| (! type)
| (type @ path-elem ... index)
| (! type @ path-elem ... index)
| (and proposition ...)
| (or proposition ...)
| (implies proposition ...)

path-elem = car
| cdr

index = positive-integer
| (positive-integer positive-integer)
| identifier

The type of functions from the (possibly-empty) sequence dom .... to the rng type.

Examples:

> (λ ([x : Number]) x)
- : (-> Number Number)
#<procedure>
> (λ () 'hello)
- : (-> 'hello)
#<procedure>

The second form specifies a uniform rest argument of type rest, and the third form specifies a non-uniform rest argument of type rest with bound bound. The bound refers to the type variable that is in scope within the rest argument type.

Examples:

> (λ ([x : Number] y : String *) (length y))
- : (-> Number String * Index)
#<procedure>
> ormap
- : (All (a c b ...)
(-> (-> a b ... b c) (Listof a) (Listof b) ... b (U False c)))
#<procedure:ormap>

In the third form, the ... introduced by ooo is literal, and bound must be an identifier denoting a type variable.

The doms can include both mandatory and optional keyword arguments. Mandatory keyword arguments are a pair of keyword and type, while optional arguments are surrounded by a pair of parentheses.

Examples:

> (:print-type file->string)
(-> Path-String [#:mode (U 'binary 'text)] String)
> (: is-zero? : (-> Number #:equality (-> Number Number Any) [#:zero Number] Any))
> (define (is-zero? n #:equality equality #:zero [zero 0])
(equality n zero))
> (is-zero? 2 #:equality =)
- : Any
#f
> (is-zero? 2 #:equality eq? #:zero 2.0)
- : Any
#f

When opt-proposition is provided, it specifies the proposition for the function type (for an introduction to propositions in Typed Racket, see Propositions and Predicates). For almost all use cases, only the simplest form of propositions, with a single type after a :, are necessary:

Example:

> string?
- : (-> Any Boolean : String)
#<procedure:string?>

The proposition specifies that when (string? x) evaluates to a true value for a conditional branch, the variable x in that branch can be assumed to have type String. Likewise, if the expression evaluates to #f in a branch, the variable does not have type String.

In some cases, asymmetric type information is useful in the propositions. For example, the filter function’s first argument is specified with only a positive proposition:

Example:

> filter
- : (All (a b)
      (case->
       (-> (-> a Any : #:+ b) (Listof a) (Listof b))
       (-> (-> a Any) (Listof a) (Listof a))))
#<procedure:filter>

The use of #:+ indicates that when the function applied to a variable evaluates to a true value, the given type can be assumed for the variable. However, the type-checker gains no information in branches in which the result is #f.

Conversely, #:- specifies that a function provides information for the false branch of a conditional.

The other proposition cases are rarely needed, but the grammar documents them for completeness. They correspond to logical operations on the propositions.

The type of functions can also be specified with an infix -> which comes immediately before the rng type. The fourth through sixth forms match the first three cases, but with the infix style of arrow.

Examples:

> (: add2 (Number -> Number))
> (define (add2 n) (+ n 2))

syntax
(->* (mandatory-dom ...) optional-doms rest rng)

mandatory-dom = type
| keyword type

optional-doms =
| (optional-dom ...)

optional-dom = type
| keyword type

rest =
| #:rest type

Constructs the type of functions with optional or rest arguments. The first list of mandatory-doms correspond to mandatory argument types. The list optional-doms, if provided, specifies the optional argument types.

Examples:

> (: append-bar (->* (String) (Positive-Integer) String))
> (define (append-bar str [how-many 1])
(apply string-append str (make-list how-many "bar")))

If provided, the rest expression specifies the type of elements in the rest argument list.

Examples:

> (: +all (->* (Integer) #:rest Integer (Listof Integer)))
> (define (+all inc . rst)
(map (λ ([x : Integer]) (+ x inc)) rst))
> (+all 20 1 2 3)
- : (Listof Integer)
'(21 22 23)

Both the mandatory and optional argument lists may contain keywords paired with types.

Examples:

> (: kw-f (->* (#:x Integer) (#:y Integer) Integer))
> (define (kw-f #:x x #:y [y 0]) (+ x y))

The syntax for this type constructor matches the syntax of the ->* contract combinator, but with types instead of contracts.

syntax
Top
syntax
Bot

These are propositions that can be used with ->. Top is the propositions with no information. Bot is the propositions which means the result cannot happen.

syntax
Procedure

is the supertype of all function types. The Procedure type corresponds to values that satisfy the procedure? predicate. Because this type encodes only the fact that the value is a procedure, and not its argument types or even arity, the type-checker cannot allow values of this type to be applied.

For the types of functions with known arity and argument types, see the -> type constructor.

Examples:

> (: my-list Procedure)
> (define my-list list)
> (my-list "zwiebelkuchen" "socca")
eval:85:0: Type Checker: cannot apply a function with
unknown arity;
function `my-list' has type Procedure which cannot be
applied
in: "socca"

syntax
(U t ...)

is the union of the types t ....

Example:

> (λ ([x : Real]) (if (> 0 x) "yes" 'no))
- : (-> Real (U 'no String))
#<procedure>

syntax
(∩ t ...)

is the intersection of the types t ....

Example:

> ((λ #:forall (A) ([x : (∩ Symbol A)]) x) 'foo)
- : Symbol [more precisely: 'foo]
'foo

syntax
(case-> fun-ty ...)

is a function that behaves like all of the fun-tys, considered in order from first to last. The fun-tys must all be function types constructed with ->.

Example:

> (: add-map : (case->
[(Listof Integer) -> (Listof Integer)]
[(Listof Integer) (Listof Integer) -> (Listof Integer)]))

For the definition of add-map look into case-lambda:.

syntax
(t t1 t2 ...)

is the instantiation of the parametric type t at types t1 t2 ...

syntax
(All (a ...) t)
(All (a ... a ooo) t)

is a parameterization of type t, with type variables a .... If t is a function type constructed with infix ->, the outer pair of parentheses around the function type may be omitted.

Examples:

> (: list-length : (All (A) (Listof A) -> Natural))
> (define (list-length lst)
    (if (null? lst)
        0
        (add1 (list-length (cdr lst)))))
> (list-length (list 1 2 3))
- : Integer [more precisely: Nonnegative-Integer]
3

syntax
(Values t ...)

is the type of a sequence of multiple values, with types t .... This can only appear as the return type of a function.

Example:

> (values 1 2 3)
- : (values Integer Integer Integer) [more precisely: (Values One Positive-Byte Positive-Byte)]
1
2
3

Note that a type variable cannot be instantiated with a (Values ....) type. For example, the type (All (A) (-> A)) describes a thunk that returns exactly one value.

syntax
v

where v is a number, boolean or string, is the singleton type containing only that value

syntax
(quote val)

where val is a Racket value, is the singleton type containing only that value

syntax
i

where i is an identifier can be a reference to a type name or a type variable

syntax
(Rec n t)

is a recursive type where n is bound to the recursive type in the body t

Examples:

> (define-type IntList (Rec List (Pair Integer (U List Null))))
> (define-type (List A) (Rec List (Pair A (U List Null))))

syntax
(Struct st)

is a type which is a supertype of all instances of the potentially-polymorphic structure type st. Note that structure accessors for st will not accept (Struct st) as an argument.

syntax
(Struct-Type st)

is a type for the structure type descriptor value for the structure type st. Values of this type are used with reflective operations such as struct-type-info.

Examples:

> struct:arity-at-least
- : (StructType arity-at-least)
#<struct-type:arity-at-least>
> (struct-type-info struct:arity-at-least)
- : (values
     Symbol
     Integer
     Integer
     (-> arity-at-least Nonnegative-Integer Any)
     (-> arity-at-least Nonnegative-Integer Nothing Void)
     (Listof Nonnegative-Integer)
     (U False Struct-TypeTop)
     Boolean)
[more precisely: (values
                  Symbol
                  Nonnegative-Integer
                  Nonnegative-Integer
                  (-> arity-at-least Nonnegative-Integer Any)
                  (-> arity-at-least Nonnegative-Integer Nothing Void)
                  (Listof Nonnegative-Integer)
                  (U False Struct-TypeTop)
                  Boolean)]
'arity-at-least
1
0
#<procedure:arity-at-least-ref>
#<procedure:arity-at-least-set!>
'(0)
#f
#f

syntax
Struct-TypeTop

is the supertype of all types for structure type descriptor values. The corresponding structure type is unknown for values of this top type.

Example:

> (struct-info (arity-at-least 0))
- : (values (U False Struct-TypeTop) Boolean)
#<struct-type:arity-at-least>
#f

syntax
(Prefab key type ...)

Represents a prefab structure type with the given prefab structure key (such as one returned by prefab-struct-key or accepted by make-prefab-struct) and with the given types for each field.

In the case of prefab structure types with supertypes, the field types of the supertypes come before the field types of the child structure type. The order of types matches the order of arguments to a prefab struct constructor.

Examples:

> #s(salad "potato" "mayo")
- : (Prefab salad String String)
'#s(salad "potato" "mayo")
> (: q-salad (Prefab (salad food 1) String String Symbol))
> (define q-salad
#s((salad food 1) "quinoa" "EVOO" salad))

syntax
Union

An alias for U.

syntax
Intersection

An alias for ∩.

syntax
→

An alias for ->.

syntax
case→

An alias for case->.

syntax
∀

An alias for All.

1.7 Other Types

syntax
(Option t)

Either t or #f

syntax
(Opaque t)

A type constructed using the #:opaque clause of require/typed.

top ← prev up next →

1	Type Reference
2	Special Form Reference
3	Libraries Provided With Typed Racket
4	Typed Classes
5	Typed Units
6	Utilities
7	Exploring Types
8	Typed Racket Syntax Without Type Checking
9	Typed Regions
10	Optimization in Typed Racket
11	Unsafe Typed Racket operations
12	Legacy Forms
13	Compatibility Languages
14	Experimental Features

1.1	Base Types
1.2	Singleton Types
1.3	Containers
1.4	Syntax Objects
1.5	Control
1.6	Other Type Constructors
1.7	Other Types