9.5 Real Distribution Families

The distribution object constructors documented in this section return uniquely defined distributions for the largest possible parameter domain. This usually means that they return distributions for a larger domain than their mathematical counterparts are defined on.

For example, those that have a scale parameter, such as cauchy-dist, logistic-dist, exponential-dist and normal-dist, are typically undefined for a zero scale. However, in floating-point math, it is often useful to simulate limits in finite time using special values like +inf.0. Therefore, when a scale-parameterized family’s constructor receives 0, it returns a distribution object that behaves like a Delta-Dist:

> (pdf (normal-dist 1 0) 1)
+inf.0
> (pdf (normal-dist 1 0) 1.0000001)
0.0

Further, negative scales are accepted, even for exponential-dist, which results in a distribution with positive scale reflected about zero.

Some parameters’ boundary values give rise to non-unique limits. Sometimes the ambiguity can be resolved using necessary properties; see Gamma-Dist for an example. When no resolution exists, as with (beta-dist 0 0), which puts an indeterminate probability on the value 0 and the rest on 1, the constructor returns an undefined distribution.

Some distribution object constructors attempt to return sensible distributions when given special values such as +inf.0 as parameters. Do not count on these yet.

Many distribution families, such as Gamma-Dist, can be parameterized on either scale or rate (which is the reciprocal of scale). In all such cases, the implementations provided by math/distributions are parameterized on scale.

9.5.1 Beta Distributions

Wikipedia: Beta Distribution.

syntax
Beta-Dist
procedure
(beta-dist alpha beta) → Beta-Dist
  alpha : Real
  beta : Real
procedure
(beta-dist-alpha d) → Flonum
  d : Beta-Dist
procedure
(beta-dist-beta d) → Flonum
  d : Beta-Dist

Represents the beta distribution family parameterized by two shape parameters, or pseudocounts, which must both be nonnegative.

Examples:

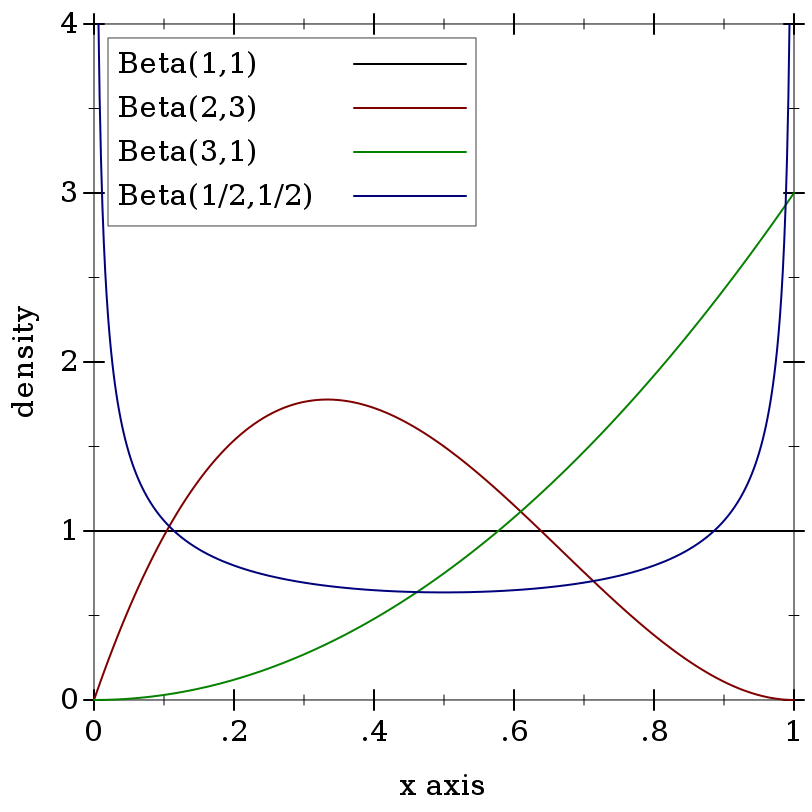
> (plot (for/list ([α  (in-list '(1 2 3 1/2))]
                   [β  (in-list '(1 3 1 1/2))]
                   [i  (in-naturals)])
          (function (distribution-pdf (beta-dist α β))
                    #:color i #:label (format "Beta(~a,~a)" α β)))
        #:x-min 0 #:x-max 1 #:y-max 4 #:y-label "density")
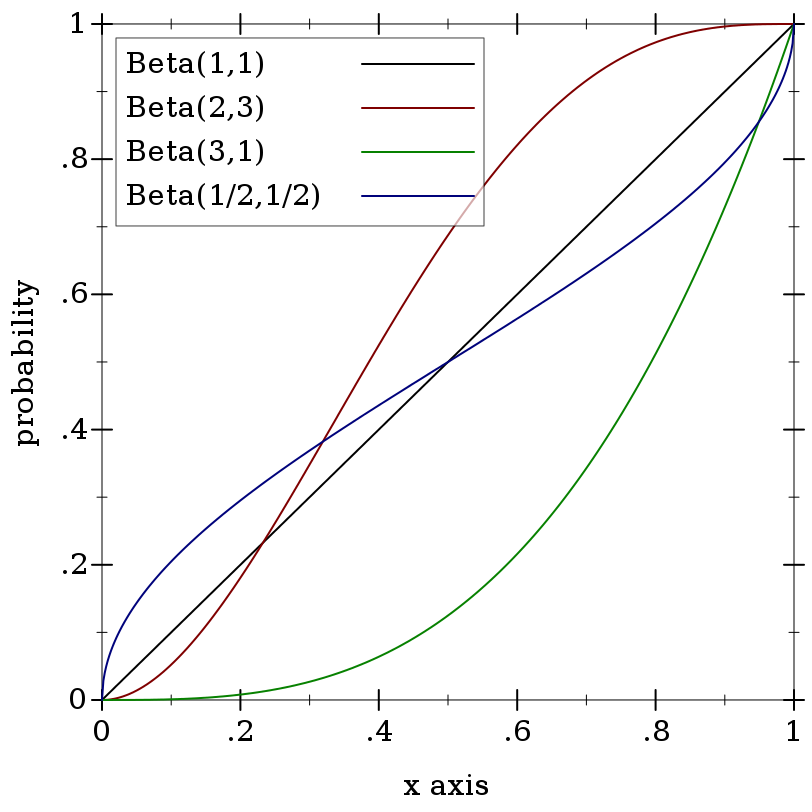
> (plot (for/list ([α  (in-list '(1 2 3 1/2))]
                   [β  (in-list '(1 3 1 1/2))]
                   [i  (in-naturals)])
          (function (ordered-dist-cdf (beta-dist α β))
                    #:color i #:label (format "Beta(~a,~a)" α β)))
        #:x-min 0 #:x-max 1 #:y-label "probability")

(beta-dist 0 0) and (beta-dist +inf.0 +inf.0) are undefined distributions.

When a = 0 or b = +inf.0, the returned distribution acts like (delta-dist 0).

When a = +inf.0 or b = 0, the returned distribution acts like (delta-dist 1).

9.5.2 Cauchy Distributions

Wikipedia: Cauchy Distribution.

syntax
Cauchy-Dist
procedure
(cauchy-dist [mode scale]) → Cauchy-Dist
  mode : Real = 0
  scale : Real = 1
procedure
(cauchy-dist-mode d) → Flonum
  d : Cauchy-Dist
procedure
(cauchy-dist-scale d) → Flonum
  d : Cauchy-Dist

Represents the Cauchy distribution family parameterized by mode and scale.

Examples:

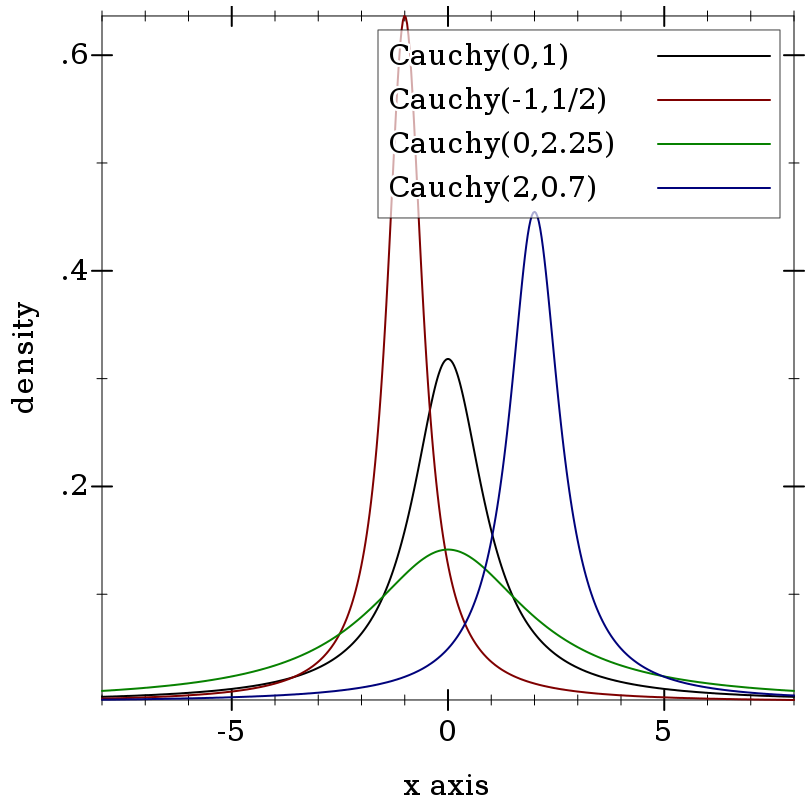
> (plot (for/list ([m  (in-list '(0 -1 0 2))]
                   [s  (in-list '(1 1/2 2.25 0.7))]
                   [i  (in-naturals)])
          (function (distribution-pdf (cauchy-dist m s))
                    #:color i #:label (format "Cauchy(~a,~a)" m s)))
        #:x-min -8 #:x-max 8 #:y-label "density"
        #:legend-anchor 'top-right)
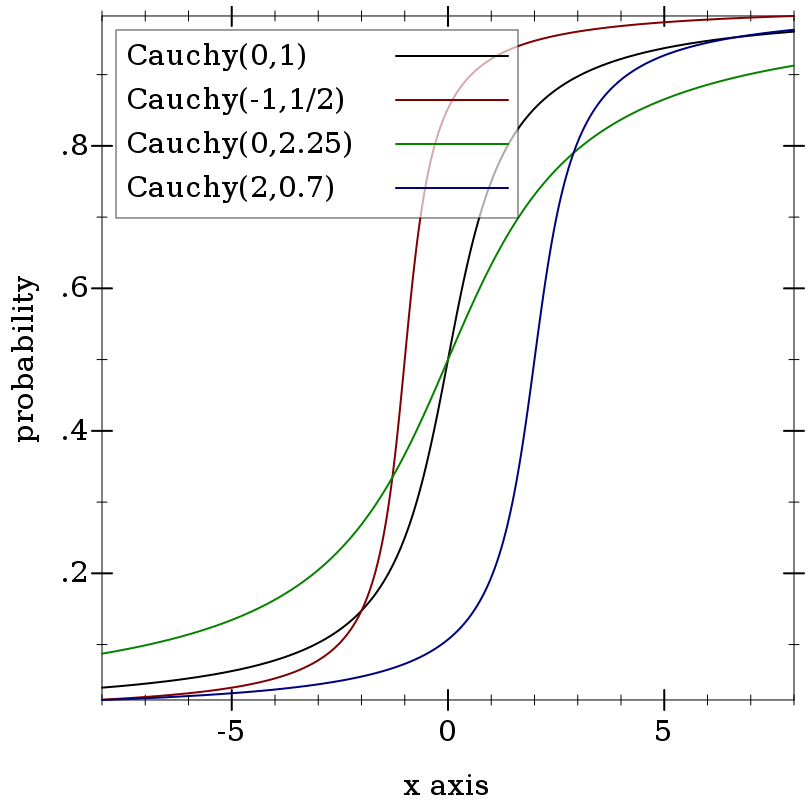
> (plot (for/list ([m  (in-list '(0 -1 0 2))]
                   [s  (in-list '(1 1/2 2.25 0.7))]
                   [i  (in-naturals)])
          (function (ordered-dist-cdf (cauchy-dist m s))
                    #:color i #:label (format "Cauchy(~a,~a)" m s)))
        #:x-min -8 #:x-max 8 #:y-label "probability")

9.5.3 Delta Distributions

Wikipedia: Dirac Delta Function.

syntax
Delta-Dist
procedure
(delta-dist [mean]) → Delta-Dist
mean : Real = 0
procedure
(delta-dist-mean d) → Flonum
d : Delta-Dist

Represents the family of distributions whose densities are Dirac delta functions.

Examples:

> (pdf (delta-dist) 0)
+inf.0
> (pdf (delta-dist) 1)
0.0
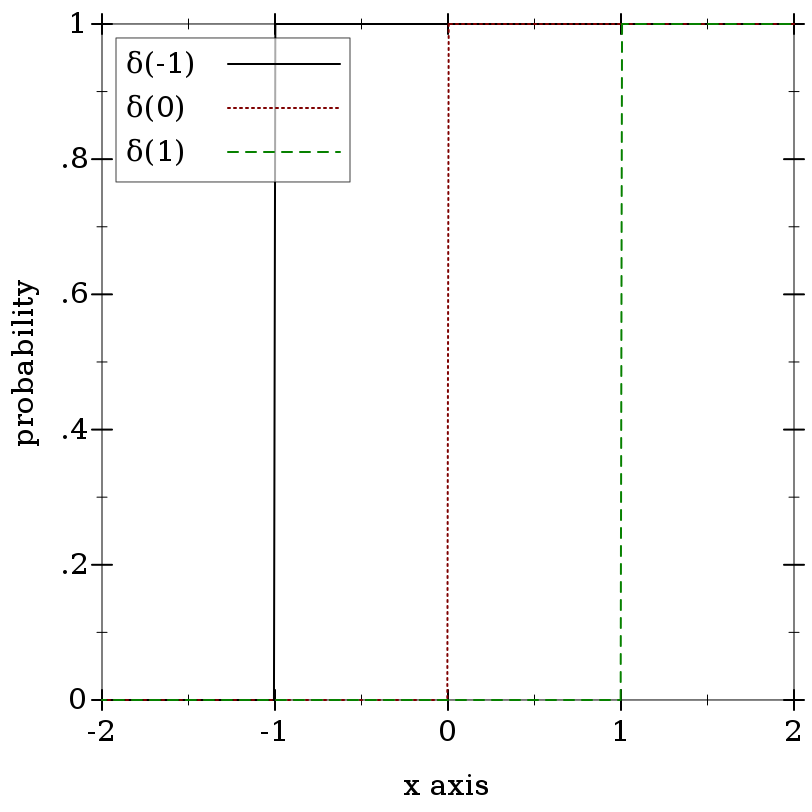
> (plot (for/list ([μ  (in-list '(-1 0 1))]
                   [i  (in-naturals)])
          (function (ordered-dist-cdf (delta-dist μ))
                    #:color i #:style i #:label (format "δ(~a)" μ)))
        #:x-min -2 #:x-max 2 #:y-label "probability")

9.5.4 Exponential Distributions

Wikipedia: Exponential Distribution.

syntax
Exponential-Dist
procedure
(exponential-dist [mean]) → Exponential-Dist
mean : Real = 1
procedure
(exponential-dist-mean d) → Flonum
d : Exponential-Dist

Represents the exponential distribution family parameterized by mean, or scale.

Warning: The exponential distribution family is often parameterized by rate, which is the reciprocal of mean or scale. Construct exponential distributions from rates using

(exponential-dist (/ 1.0 rate))

Examples:

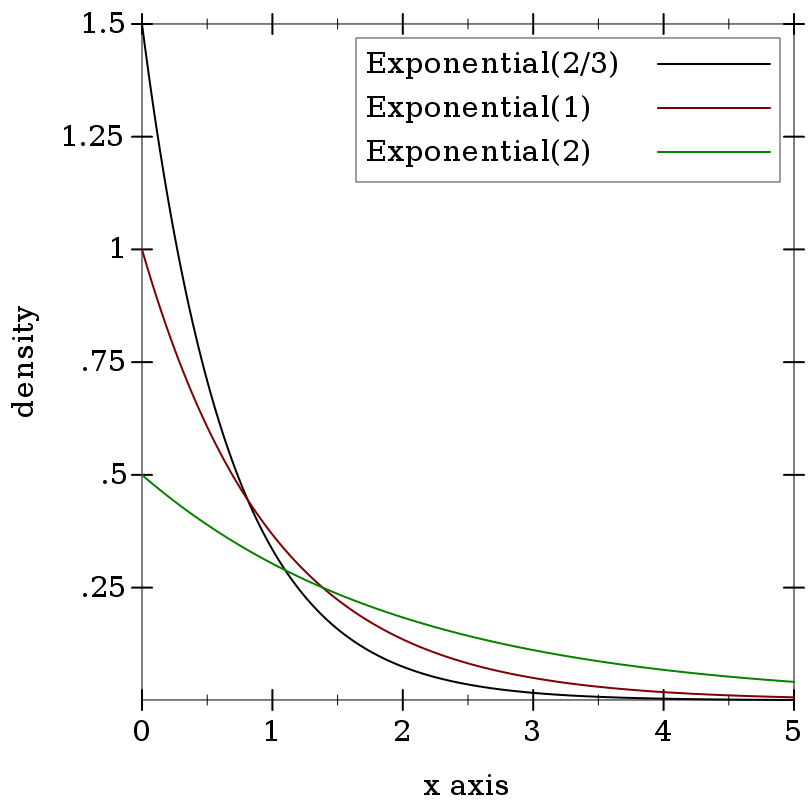
> (plot (for/list ([μ  (in-list '(2/3 1 2))]
                   [i  (in-naturals)])
          (function (distribution-pdf (exponential-dist μ))
                    #:color i #:label (format "Exponential(~a)" μ)))
        #:x-min 0 #:x-max 5 #:y-label "density"
        #:legend-anchor 'top-right)
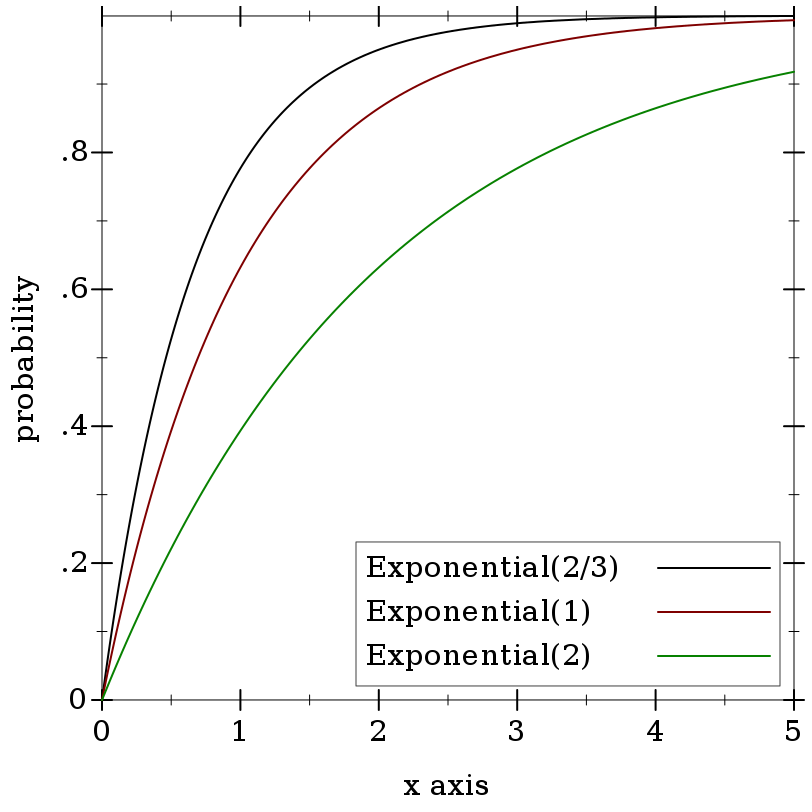
> (plot (for/list ([μ  (in-list '(2/3 1 2))]
                   [i  (in-naturals)])
          (function (ordered-dist-cdf (exponential-dist μ))
                    #:color i #:label (format "Exponential(~a)" μ)))
        #:x-min 0 #:x-max 5 #:y-label "probability"
        #:legend-anchor 'bottom-right)

9.5.5 Gamma Distributions

Wikipedia: Gamma Distribution.

syntax
Gamma-Dist
procedure
(gamma-dist [shape scale]) → Gamma-Dist
  shape : Real = 1
  scale : Real = 1
procedure
(gamma-dist-shape d) → Flonum
  d : Gamma-Dist
procedure
(gamma-dist-scale d) → Flonum
  d : Gamma-Dist

Represents the gamma distribution family parameterized by shape and scale. The shape parameter must be nonnegative.

Warning: The gamma distribution family is often parameterized by shape and rate, which is the reciprocal of scale. Construct gamma distributions from rates using

(gamma-dist shape (/ 1.0 rate))

Examples:

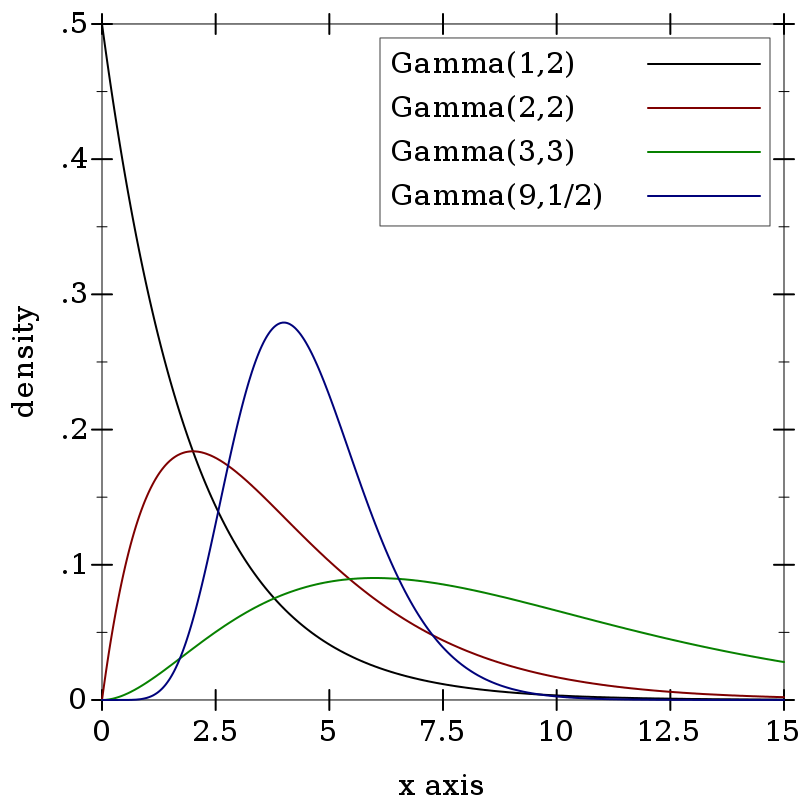
> (plot (for/list ([k  (in-list '(1 2 3 9))]
                   [s  (in-list '(2 2 3 1/2))]
                   [i  (in-naturals)])
          (function (distribution-pdf (gamma-dist k s))
                    #:color i #:label (format "Gamma(~a,~a)" k s)))
        #:x-min 0 #:x-max 15 #:y-label "density"
        #:legend-anchor 'top-right)
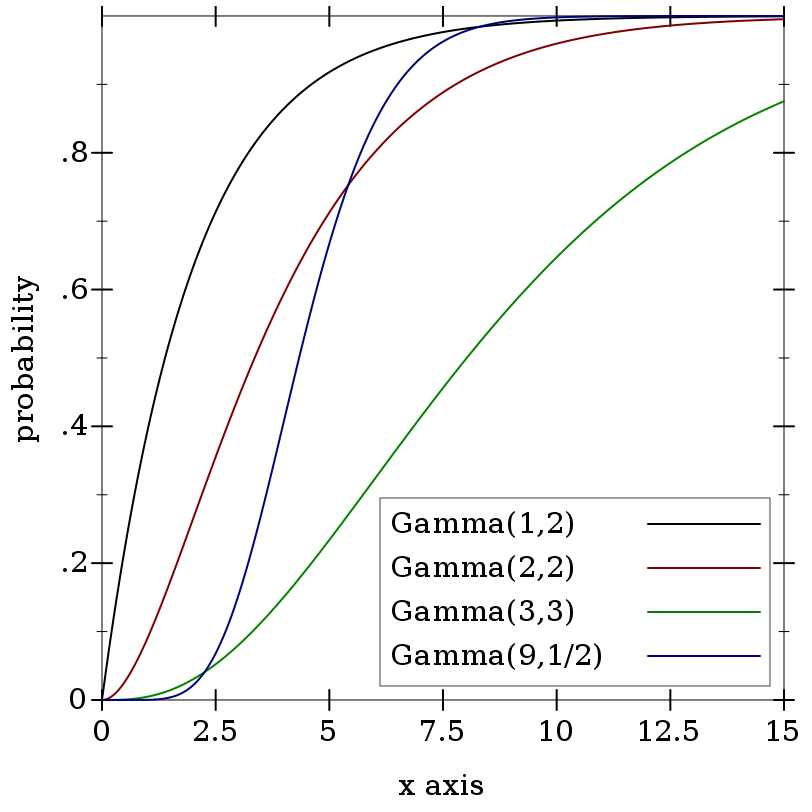
> (plot (for/list ([k  (in-list '(1 2 3 9))]
                   [s  (in-list '(2 2 3 1/2))]
                   [i  (in-naturals)])
          (function (ordered-dist-cdf (gamma-dist k s))
                    #:color i #:label (format "Gamma(~a,~a)" k s)))
        #:x-min 0 #:x-max 15 #:y-label "probability"
        #:legend-anchor 'bottom-right)

The cdf of the gamma distribution with shape = 0 could return either 0.0 or 1.0 at x = 0, depending on whether a double limit is taken with respect to scale or with respect to x first. However the limits are taken, the cdf must return 1.0 for x > 0. Because cdfs are right-continuous, the only correct choice is

> (cdf (gamma-dist 0 1) 0)
1.0

Therefore, a gamma distribution with shape = 0 behaves like (delta-dist 0).

9.5.6 Logistic Distributions

Wikipedia: Logistic Distribution.

syntax
Logistic-Dist
procedure
(logistic-dist [mean scale]) → Logistic-Dist
  mean : Real = 0
  scale : Real = 1
procedure
(logistic-dist-mean d) → Flonum
  d : Logistic-Dist
procedure
(logistic-dist-scale d) → Flonum
  d : Logistic-Dist

Represents the logistic distribution family parameterized by mean (also called “location”) and scale. In this parameterization, the variance is (* 1/3 (sqr (* pi scale))).

Examples:

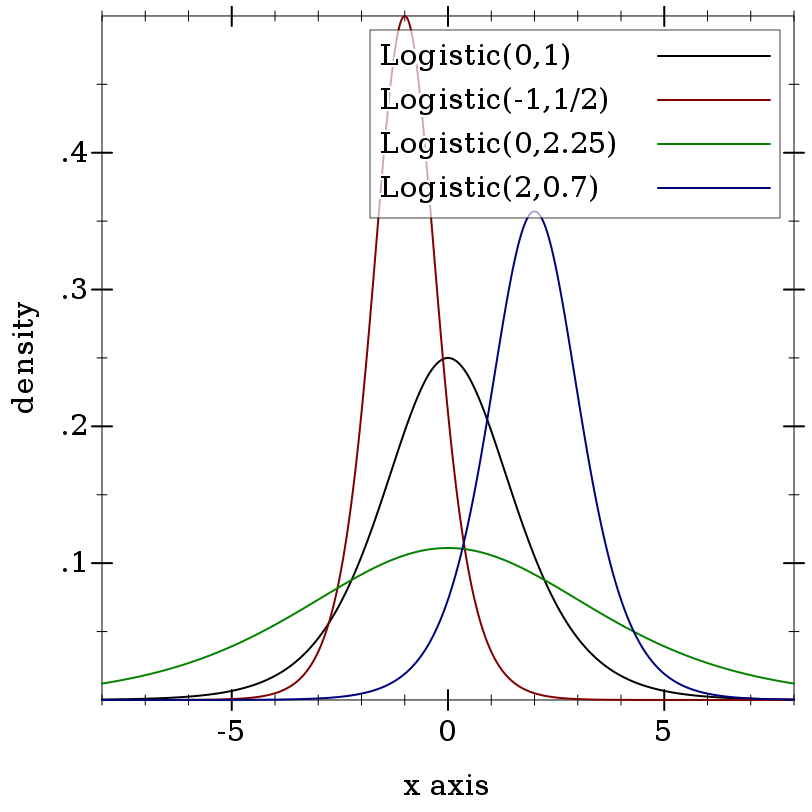
> (plot (for/list ([μ  (in-list '(0 -1 0 2))]
                   [s  (in-list '(1 1/2 2.25 0.7))]
                   [i  (in-naturals)])
          (function (distribution-pdf (logistic-dist μ s))
                    #:color i #:label (format "Logistic(~a,~a)" μ s)))
        #:x-min -8 #:x-max 8 #:y-label "density"
        #:legend-anchor 'top-right)
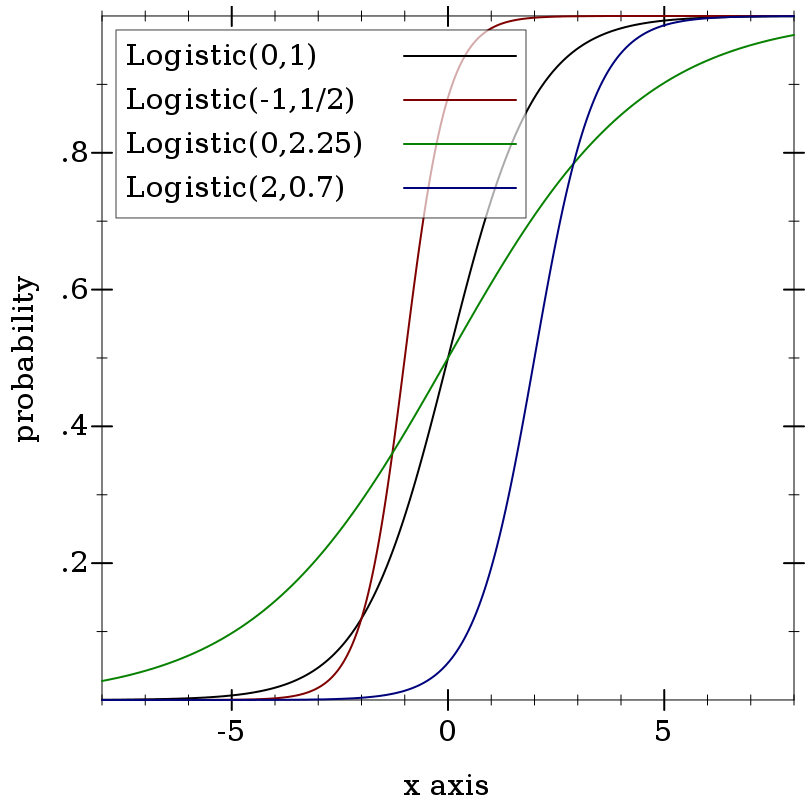
> (plot (for/list ([μ  (in-list '(0 -1 0 2))]
                   [s  (in-list '(1 1/2 2.25 0.7))]
                   [i  (in-naturals)])
          (function (ordered-dist-cdf (logistic-dist μ s))
                    #:color i #:label (format "Logistic(~a,~a)" μ s)))
        #:x-min -8 #:x-max 8 #:y-label "probability")

9.5.7 Normal Distributions

Wikipedia: Normal Distribution.

syntax
Normal-Dist
procedure
(normal-dist [mean stddev]) → Normal-Dist
  mean : Real = 0
  stddev : Real = 1
procedure
(normal-dist-mean d) → Flonum
  d : Normal-Dist
procedure
(normal-dist-stddev d) → Flonum
  d : Normal-Dist

Represents the normal distribution family parameterized by mean and standard deviation.

Warning: The normal distribution family is often parameterized by mean and variance, which is the square of standard deviation. Construct normal distributions from variances using

(normal-dist mean (sqrt var))

Examples:

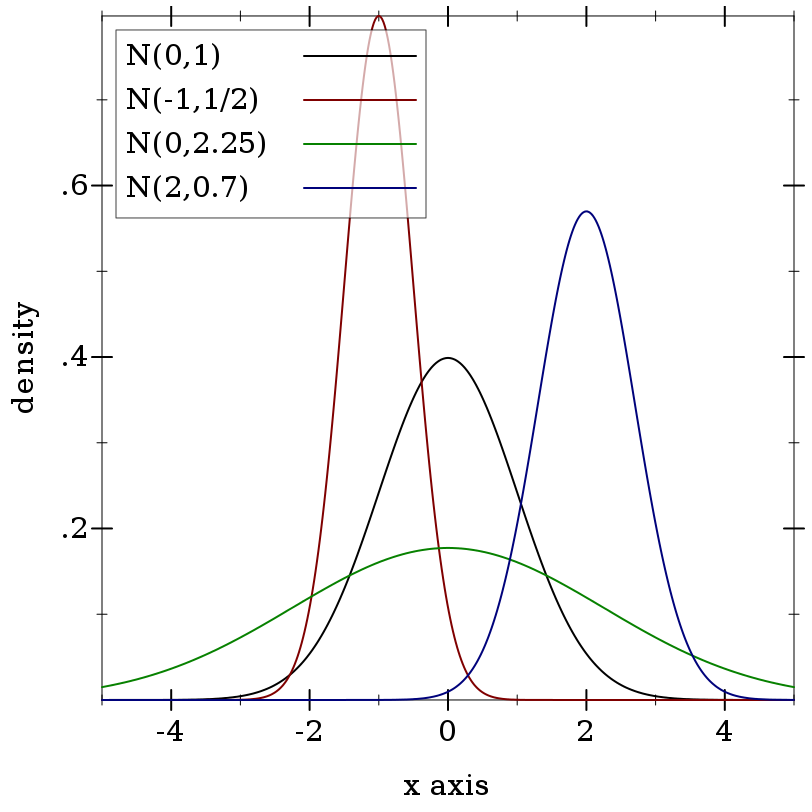
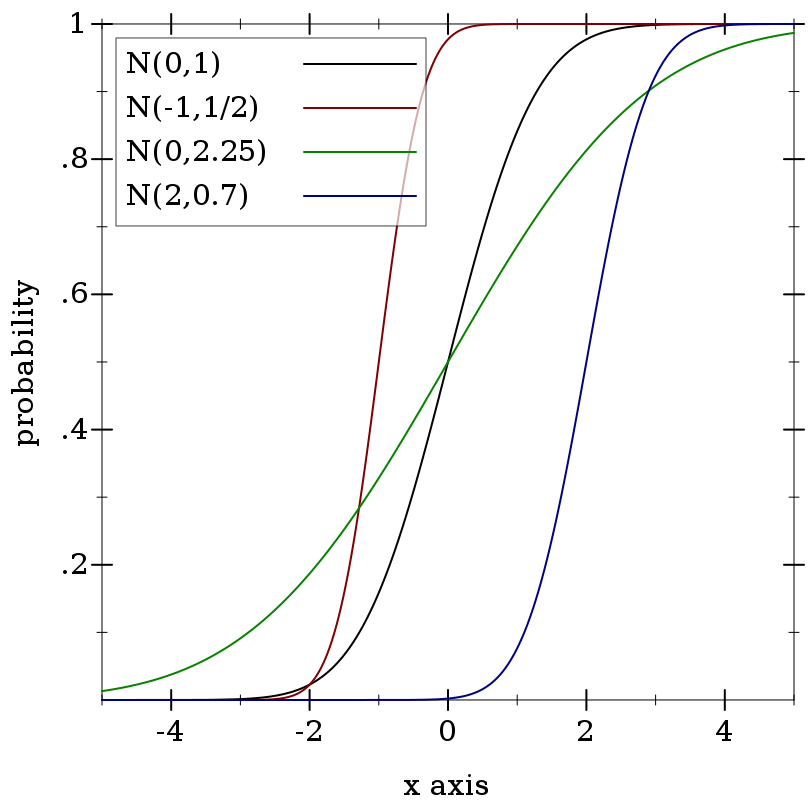
> (plot (for/list ([μ  (in-list '(0 -1 0 2))]
                   [σ  (in-list '(1 1/2 2.25 0.7))]
                   [i  (in-naturals)])
          (function (distribution-pdf (normal-dist μ σ))
                    #:color i #:label (format "N(~a,~a)" μ σ)))
        #:x-min -5 #:x-max 5 #:y-label "density")
> (plot (for/list ([μ  (in-list '(0 -1 0 2))]
                   [σ  (in-list '(1 1/2 2.25 0.7))]
                   [i  (in-naturals)])
          (function (ordered-dist-cdf (normal-dist μ σ))
                    #:color i #:label (format "N(~a,~a)" μ σ)))
        #:x-min -5 #:x-max 5 #:y-label "probability")

9.5.8 Triangular Distributions

Wikipedia: Triangular Distribution.

syntax
Triangle-Dist
procedure
(triangle-dist [min max mode]) → Triangle-Dist
  min : Real = 0
  max : Real = 1
  mode : Real = (* 0.5 (+ min max))
procedure
(triangle-dist-min d) → Flonum
  d : Triangle-Dist
procedure
(triangle-dist-max d) → Flonum
  d : Triangle-Dist
procedure
(triangle-dist-mode d) → Flonum
  d : Triangle-Dist

Represents the triangular distribution family parameterized by minimum, maximum and mode.

If min, mode and max are not in ascending order, they are sorted before constructing the distribution object.

Examples:

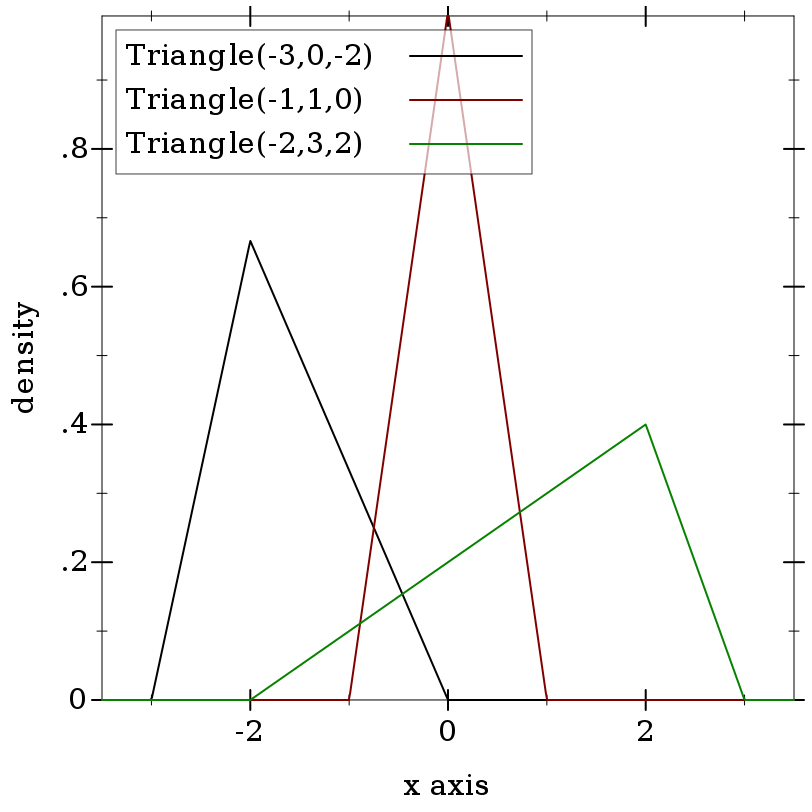
> (plot (for/list ([a  (in-list '(-3 -1 -2))]
                   [b  (in-list '(0 1 3))]
                   [m  (in-list '(-2 0 2))]
                   [i  (in-naturals)])
          (function (distribution-pdf (triangle-dist a b m)) #:color i
                    #:label (format "Triangle(~a,~a,~a)" a b m)))
        #:x-min -3.5 #:x-max 3.5 #:y-label "density")
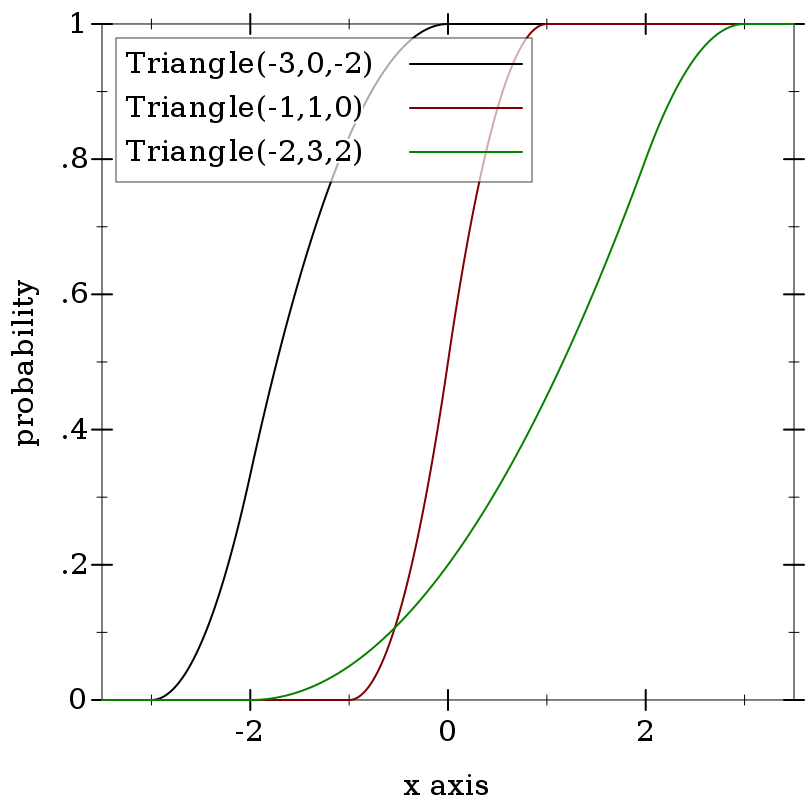
> (plot (for/list ([a  (in-list '(-3 -1 -2))]
                   [b  (in-list '(0 1 3))]
                   [m  (in-list '(-2 0 2))]
                   [i  (in-naturals)])
          (function (ordered-dist-cdf (triangle-dist a b m)) #:color i
                    #:label (format "Triangle(~a,~a,~a)" a b m)))
        #:x-min -3.5 #:x-max 3.5 #:y-label "probability")

(triangle-dist c c c) for any real c behaves like a support-limited delta distribution centered at c.

9.5.9 Truncated Distributions

syntax
Truncated-Dist
procedure
(truncated-dist d) → Truncated-Dist
  d : Real-Dist
(truncated-dist d max) → Truncated-Dist
  d : Real-Dist
  max : Real
(truncated-dist d min max) → Truncated-Dist
  d : Real-Dist
  min : Real
  max : Real
procedure
(truncated-dist-original t) → Real-Dist
  t : Truncated-Dist
procedure
(truncated-dist-min t) → Flonum
  t : Truncated-Dist
procedure
(truncated-dist-max t) → Flonum
  t : Truncated-Dist

Represents distributions like d, but with zero density for x < min and for x > max. The probability of the interval [min, max] is renormalized to one.

(truncated-dist d) is equivalent to (truncated-dist d -inf.0 +inf.0). (truncated-dist d max) is equivalent to (truncated-dist d -inf.0 max). If min > max, they are swapped before constructing the distribution object.

Samples are taken by applying the truncated distribution’s inverse cdf to uniform samples.

Examples:

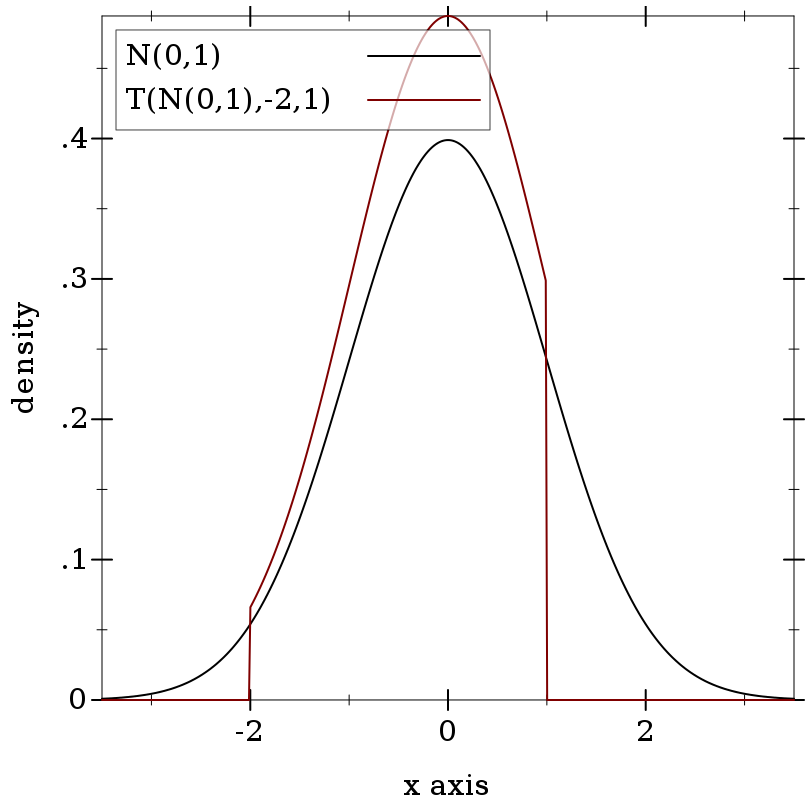
> (define d (normal-dist))
> (define t (truncated-dist d -2 1))
> t
(truncated-dist (normal-dist 0.0 1.0) -2.0 1.0)
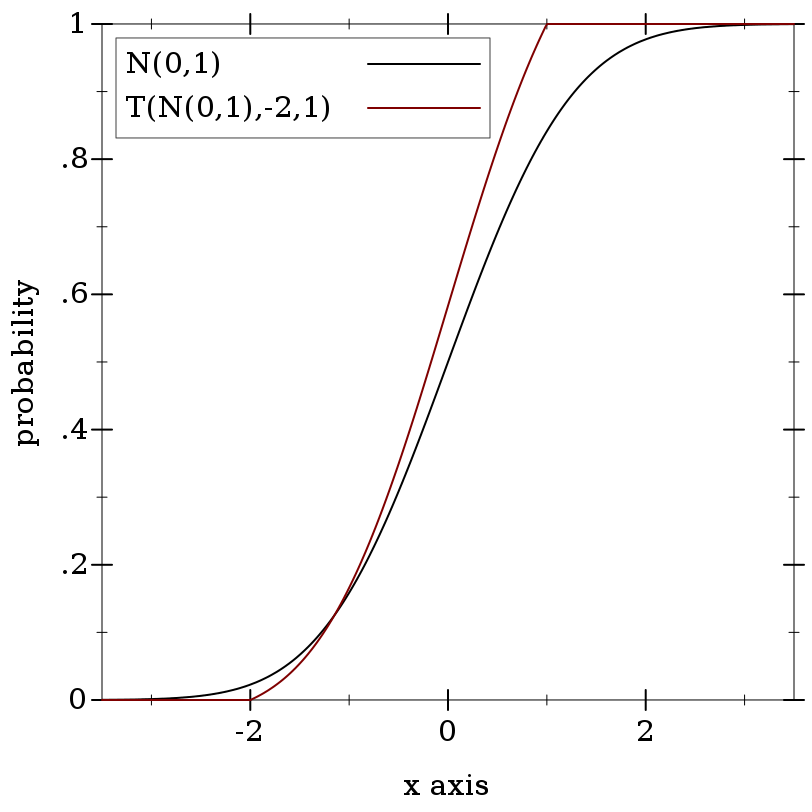
> (plot (list (function (distribution-pdf d) #:label "N(0,1)" #:color 0)
              (function (distribution-pdf t) #:label "T(N(0,1),-2,1)"))
        #:x-min -3.5 #:x-max 3.5 #:y-label "density")
> (plot (list (function (ordered-dist-cdf d) #:label "N(0,1)" #:color 0)
              (function (ordered-dist-cdf t) #:label "T(N(0,1),-2,1)"))
        #:x-min -3.5 #:x-max 3.5 #:y-label "probability")

9.5.10 Uniform Distributions

Wikipedia: Uniform Distribution.

syntax
Uniform-Dist
procedure
(uniform-dist) → Uniform-Dist
(uniform-dist max) → Uniform-Dist
  max : Real
(uniform-dist min max) → Uniform-Dist
  min : Real
  max : Real
procedure
(uniform-dist-min d) → Flonum
  d : Uniform-Dist
procedure
(uniform-dist-max d) → Flonum
  d : Uniform-Dist

Represents the uniform distribution family parameterized by minimum and maximum.

(uniform-dist) is equivalent to (uniform-dist 0 1). (uniform-dist max) is equivalent to (uniform-dist 0 max). If max < min, they are swapped before constructing the distribution object.

Examples:

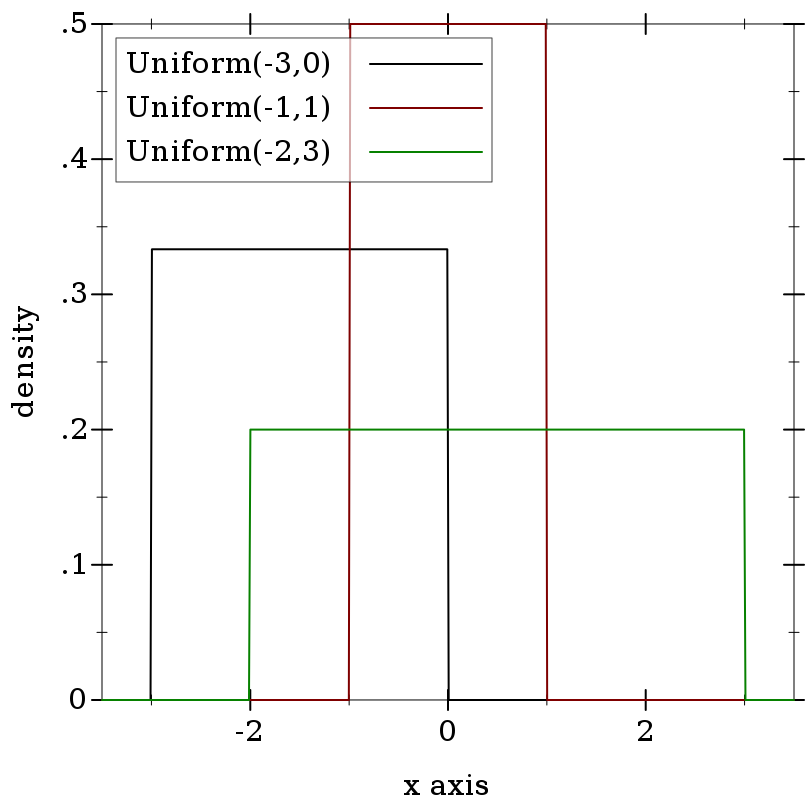
> (plot (for/list ([a  (in-list '(-3 -1 -2))]
                   [b  (in-list '(0 1 3))]
                   [i  (in-naturals)])
          (function (distribution-pdf (uniform-dist a b)) #:color i
                    #:label (format "Uniform(~a,~a)" a b)))
        #:x-min -3.5 #:x-max 3.5 #:y-label "density")
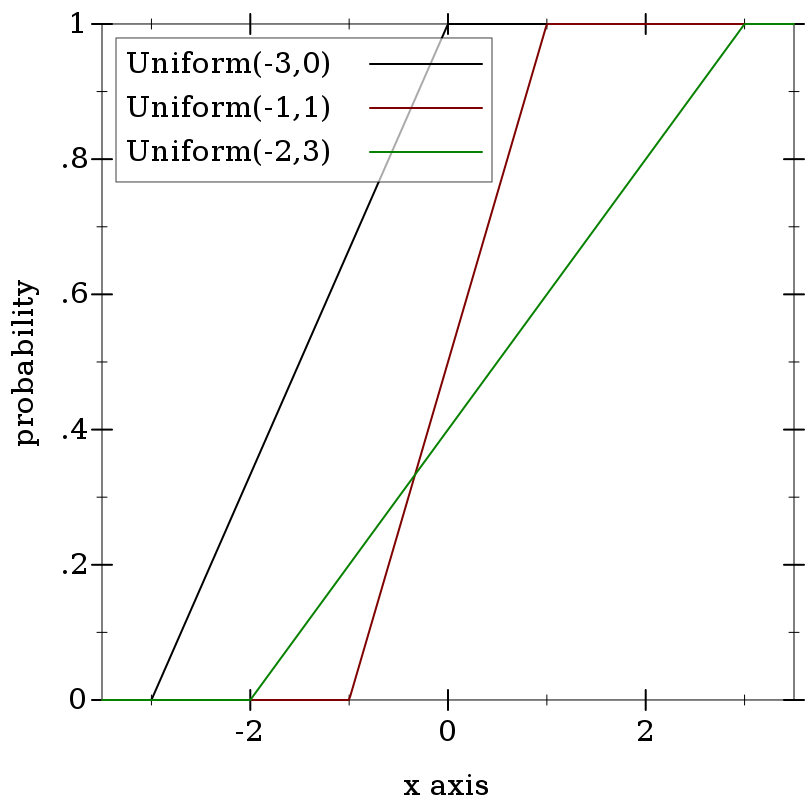
> (plot (for/list ([a  (in-list '(-3 -1 -2))]
                   [b  (in-list '(0 1 3))]
                   [i  (in-naturals)])
          (function (ordered-dist-cdf (uniform-dist a b)) #:color i
                    #:label (format "Uniform(~a,~a)" a b)))
        #:x-min -3.5 #:x-max 3.5 #:y-label "probability")

(uniform-dist x x) for any real x behaves like a support-limited delta distribution centered at x.

top ← prev up next →

1	Constants and Elementary Functions
2	Flonums
3	Special Functions
4	Number Theory
5	Arbitrary-Precision Floating-Point Numbers (Bigfloats)
6	Arrays
7	Matrices and Linear Algebra
8	Statistics Functions
9	Probability Distributions
10	Stuff That Doesn’t Belong Anywhere Else

9.1	Distribution Objects
9.2	Distribution Types and Operations
9.3	Finite Distribution Families
9.4	Integer Distribution Families
9.5	Real Distribution Families
9.6	Low-Level Distribution Functions

9.5.1	Beta Distributions
9.5.2	Cauchy Distributions
9.5.3	Delta Distributions
9.5.4	Exponential Distributions
9.5.5	Gamma Distributions
9.5.6	Logistic Distributions
9.5.7	Normal Distributions
9.5.8	Triangular Distributions
9.5.9	Truncated Distributions
9.5.10	Uniform Distributions