2 Long Tutorial

8.5

2 Long Tutorial

This tutorial is derived from a week-long Redex summer school, run July 27–31, 2015 at the University of Utah.

2.1 The Theoretical Framework

Goals

— abstract syntax

— notions of reduction, substitution

— reductions and calculations

— semantics

— standard reduction

— abstract register machines

— types

The lambda calculus:

e = x | (\x.e) | (e e)

Terms vs trees, abstract over concrete syntax

Encode some forms of primitives: numbers, booleans – good for theory of computation; mostly irrelevant for PL. extensions with primitive data

e = x | (\x.e) | (e e) | tt | ff | (if e e e)

What we want: develop LC as a model of a PL. Because of history, this means two things: a simple logic for calculating with the terms of the language e == e’ and a system for determining the value of a program. The former is the calculus, the latter is the semantics.

Both start with basic notions of reduction (axioms). They are just relation on terms:

((\x.e) e’) beta e[x=e’]

pronounced: e with x replaced by e’

((\x.e) e’) beta [e’/x]e

pronounced substitute e’ for x in e

Think substitution via tree surgery, preserving bindings

Here are two more, often done via external interpretation functions (δ)

(if tt e e’) if-tt e

(if ff e e’) if-ff e’

If this is supposed to be a theory of functions (and if expressions) we need to be able to use this relations in context

e xyz e'

--------------

e = e'

e = e' e = e' e = e'

-------------- -------------- --------------

e e'' = e' e'' e'' e = e'' e' \x.e = \x.e'

plus reflexivity, symmetry, and transitivity

for any relation xyz

Now you have an equational system. what’s it good for? you can prove such facts as

e (Y e) = (Y e)

meaning every single term has a fixpoint

All of the above is mathematics but it is just that, mathematics. It might be considered theory of computation, but it is not theory of programming languages. But we can use these ideas to create a theory of programming languages. Plotkin’s 1974 TCS paper on call-by-name versus call-by-value shows how to create a theory of programming languages.

In addition, Plotkin’s paper also sketches several research programs, mostly on scaling up his ideas to the full spectrum of languages but also on the precise connection between by-value and by-name their relationship, both at the proof-theoretical level as well as at the model-theoretic level.

Here is Plotkin’s idea as a quasi-algorithm:

Start from an abstract syntax, plus notions of scope and scope-preserving substitution. Consider closed terms Programs.
Identify a subset of expressions as Values. Use v to range over Values.
Note The complement of this set was (later) dubbed computations, due to Moggi’s work under Plotkin.
Define basic notions of reduction (axioms). Examples:
((\x.e) e’) beta-name e[x=e’]
((\x.e) v) beta-value e[x=v]
Inductively generate an equational theory from the basic notions of reduction.
This theory defines a semantics, that is, a relation eval from programs to values:
eval : Program x Value
def e eval v iff e = v
Prove that eval is a function, and you have got yourself a specification of an interpreter.
eval : Program -> Value
eval(e) = v
Note This step often reuses a variant of the Church-Rosser theorem of the mathematical theory of lambda calculus.
Prove that the calculus satisfies a Curry-Feys standard reduction property. This gives you a second semantics:
eval-standard : Program -> Value
def eval-standard(e) = v iff e standard reduces to v
The new semantics is correct:
Theorem eval-standard = eval
Standard reduction is a strategy for the lambda calculus, that is, a function that picks the next reducible expression (called redex) to reduce. Plotkin specifically uses the leftmost-outermost strategy but others may work, too.

Plotkin also shows—on an ad hoc basis—that this evaluator function is equivalent to Landin’s evaluator based on the SECD machine, an abstract register machine.

Plotkin (following Morris, 1968) uses step 6 from above to add two ideas:

The interpreter of a programming language (non-constructively) generates a theory of equivalence on phrases.
def e ~ e’ iff placing e and e’ into any context yields programs that produce the same observable behavior according to eval
Theorem ~ is the coarsest equivalence theory and thus unique.
Let’s call ~ the Truth.
Theorem e = e’ implies e ~ e’. Naturally the reverse doesn’t hold.

Matthias’s (post)dissertation research extends Plotkin’s work in two directions:

Plotkin’s “algorithm” applies to imperative programming language, especially those extending the lambda calculus syntax with (variable) assignment and non-local control operators.
Imperative Extensions explains how two of these work.
It is possible to derive useful abstract register machines from the standard reduction semantics of the programming language
Each machine M defines a new semantics:
def eval-M(e) = v iff load M with e, run, unload, yields v
For each of these functions, we can prove an equivalence theorem.
Theorem eval-M = eval-standard = eval

His work also shows how this approach greatly simplifies proofs of consistency for the semantics of programming languages and especially so-called type soundness theorems.

2.2 Syntax and Metafunctions

Goals

— Redex versus Racket

— define languages

— develop metafunctions, includes basic testing, submodules

— extend languages

— generalizing with any

2.2.1 Developing a Language

To start a program with Redex, start your file with

#lang racket
(require redex)

The define-language from specifies syntax trees via tree grammars:

(define-language Lambda
  (e ::= x
         (lambda (x ...) e)
         (e e ...))
  (x ::= variable-not-otherwise-mentioned))

The trees are somewhat concrete, which makes it easy to work with them, but it is confusing on those incredibly rare occasions when we want truly abstract syntax.

We can include literal numbers (all of Racket’s numbers, including complex) or integers (all of Racket’s integers) or naturals (all of Racket’s natural numbers)—and many other things.

After you have a syntax, use the grammar to generate instances and check them (typos do sneak in). Instances are generated with term:

> (define e1 (term y))
> (define e2 (term (lambda (y) y)))
> (define e3 (term (lambda (x y) y)))
> (define e4 (term (,e2 ,e3)))
> e4
'((lambda (y) y) (lambda (x y) y))

Mouse over define. It is not a Redex form, it comes from Racket. Take a close look at the last definition. Comma anyone?

(redex-match? Lambda e e4)

Define yourself a predicate that tests membership:

(define lambda? (redex-match? Lambda e))

Now you can formulate language tests:

(test-equal (lambda? e1) #true)
(test-equal (lambda? e2) #true)
(test-equal (lambda? e3) #true)
(test-equal (lambda? e4) #true)

(define eb1 (term (lambda (x x) y)))
(define eb2 (term (lambda (x y) 3)))

(test-equal (lambda? eb1) #false)
(test-equal (lambda? eb2) #false)

(test-results)

Make sure your language contains the terms that you want and does not contain those you want to exclude. Why should eb1 and eb2 not be in Lambda’s set of expressions?

2.2.2 Developing Metafunctions

To make basic statements about (parts of) your language, define metafunctions. Roughly, a metafunction is a function on the terms of a specific language.

We don’t want parameter sequences with repeated variables. Can we say this with a metafunction?

(define-metafunction Lambda
unique-vars : x ... -> boolean)

The second line is a Redex contract, not a type. It says unique-vars consumes a sequence of xs and produces a boolean.

How do we say we don’t want repeated variables? With patterns.

(define-metafunction Lambda
  unique-vars : x ... -> boolean
  [(unique-vars) #true]
  [(unique-vars x x_1 ... x x_2 ...) #false]
  [(unique-vars x x_1 ...) (unique-vars x_1 ...)])

Patterns are powerful. More later.

But, don’t just define metafunctions, develop them properly: state what they are about, work through examples, write down the latter as tests, then define the function.

; are the identifiers in the given sequence unique?

(module+ test
  (test-equal (term (unique-vars x y)) #true)
  (test-equal (term (unique-vars x y x)) #false))

(define-metafunction Lambda
  unique-vars : x ... -> boolean
  [(unique-vars) #true]
  [(unique-vars x x_1 ... x x_2 ...) #false]
  [(unique-vars x x_1 ...) (unique-vars x_1 ...)])

(module+ test
  (test-results))

Submodules delegate the tests to where they belong and they allow us to document functions by example.

Sadly, our language definition cannot use the unique-vars metafunction. (In order to define the metafunction, we first need to define the language.)

Fortunately, language definitions can employ more than Kleene patterns:

(define-language Lambda
  (e ::=
     x
     (lambda (x_!_ ...) e)
     (e e ...))
  (x ::= variable-not-otherwise-mentioned))

x_!_ ... means x must differ from all other elements of this sequence

Here are two more metafunctions that use patterns in interesting ways:

; (subtract (x ...) x_1 ...) removes x_1 ... from (x ...)

(module+ test
  (test-equal (term (subtract (x y z x) x z)) (term (y))))

(define-metafunction Lambda
  subtract : (x ...) x ... -> (x ...)
  [(subtract (x ...)) (x ...)]
  [(subtract (x ...) x_1 x_2 ...)
   (subtract (subtract1 (x ...) x_1) x_2 ...)])

; (subtract1 (x ...) x_1) removes x_1  from (x ...)
(module+ test
  (test-equal (term (subtract1 (x y z x) x)) (term (y z))))

(define-metafunction Lambda
  subtract1 : (x ...) x -> (x ...)
  [(subtract1 (x_1 ... x x_2 ...) x)
   (x_1 ... x_2new ...)
   (where (x_2new ...) (subtract1 (x_2 ...) x))
   (where #false (in x (x_1 ...)))]
  [(subtract1 (x ...) x_1) (x ...)])

(define-metafunction Lambda
  in : x (x ...) -> boolean
  [(in x (x_1 ... x x_2 ...)) #true]
  [(in x (x_1 ...)) #false])

2.2.3 Developing a Language 2

One of the first things a language designer ought to specify is scope. People often do so with a free-variables function that specifies which language constructs bind and which ones don’t:

; (fv e) computes the sequence of free variables of e
; a variable occurrence of x is free in e
; if no (lambda (... x ...) ...) dominates its occurrence

(module+ test
  (test-equal (term (fv x)) (term (x)))
  (test-equal (term (fv (lambda (x) x))) (term ()))
  (test-equal (term (fv (lambda (x) (y z x)))) (term (y z))))

(define-metafunction Lambda
  fv : e -> (x ...)
  [(fv x) (x)]
  [(fv (lambda (x ...) e))
   (subtract (x_e ...) x ...)
   (where (x_e ...) (fv e))]
  [(fv (e_f e_a ...))
   (x_f ... x_a ... ...)
   (where (x_f ...) (fv e_f))
   (where ((x_a ...) ...) ((fv e_a) ...))])

You may know it as the de Bruijn index representation.

The best approach is to specify an α equivalence relation, that is, the relation that virtually eliminates variables from phrases and replaces them with arrows to their declarations. In the world of lambda calculus-based languages, this transformation is often a part of the compiler, the so-called static-distance phase.

The function is a good example of accumulator-functions in Redex:

; (sd e) computes the static distance version of e

(define-extended-language SD Lambda
  (e ::= .... (K n))
  (n ::= natural))

(define sd1 (term (K 1)))
(define sd2 (term 1))

(define SD? (redex-match? SD e))

(module+ test
  (test-equal (SD? sd1) #true))

We have to add a means to the language to say “arrow back to the variable declaration.” We do not edit the language definition but extend the language definition instead.

(define-metafunction SD
  sd : e -> e
  [(sd e_1) (sd/a e_1 ())])

(module+ test
  (test-equal (term (sd/a x ())) (term x))
  (test-equal (term (sd/a x ((y) (z) (x)))) (term (K 2 0)))
  (test-equal (term (sd/a ((lambda (x) x) (lambda (y) y)) ()))
              (term ((lambda () (K 0 0)) (lambda () (K 0 0)))))
  (test-equal (term (sd/a (lambda (x) (x (lambda (y) y))) ()))
              (term (lambda () ((K 0 0) (lambda () (K 0 0))))))
  (test-equal (term (sd/a (lambda (z x) (x (lambda (y) z))) ()))
              (term (lambda () ((K 0 1) (lambda () (K 1 0)))))))

(define-metafunction SD
  sd/a : e ((x ...) ...) -> e
  [(sd/a x ((x_1 ...) ... (x_0 ... x x_2 ...) (x_3 ...) ...))
   ; bound variable
   (K n_rib n_pos)
   (where n_rib ,(length (term ((x_1 ...) ...))))
   (where n_pos ,(length (term (x_0 ...))))
   (where #false (in x (x_1 ... ...)))]
  [(sd/a (lambda (x ...) e_1) (e_rest ...))
   (lambda () (sd/a e_1 ((x ...) e_rest ...)))]
  [(sd/a (e_fun e_arg ...) (e_rib ...))
   ((sd/a e_fun (e_rib ...)) (sd/a e_arg (e_rib ...)) ...)]
  [(sd/a e_1 any)
   ; a free variable is left alone
   e_1])

Now α equivalence is straightforward:

; (=α e_1 e_2) determines whether e_1 and e_2 are α equivalent

(define-extended-language Lambda/n Lambda
  (e ::= .... n)
  (n ::= natural))

(define in-Lambda/n? (redex-match? Lambda/n e))

(module+ test
  (test-equal (term (=α (lambda (x) x) (lambda (y) y))) #true)
  (test-equal (term (=α (lambda (x) (x 1)) (lambda (y) (y 1)))) #true)
  (test-equal (term (=α (lambda (x) x) (lambda (y) z))) #false))

(define-metafunction SD
  =α : e e -> boolean
  [(=α e_1 e_2) ,(equal? (term (sd e_1)) (term (sd e_2)))])

(define (=α/racket x y) (term (=α ,x ,y)))

2.2.4 Extending a Language: any

Suppose we wish to extend Lambda with if and Booleans, like this:

(define-extended-language SD Lambda
  (e ::= ....
     true
     false
     (if e e e)))

Guess what? (term (fv (lambda (x y) (if x y false)))) doesn’t work because false and if are not covered.

We want metafunctions that are as generic as possible for computing such notions as free variable sequences, static distance, and alpha equivalences.

Redex contracts come with any and Redex patterns really are over Racket’s S-expressions. This definition now works for extensions that don’t add binders:

(module+ test
  (test-equal (SD? sd1) #true))

(define-metafunction SD
  sd : any -> any
  [(sd any_1) (sd/a any_1 ())])

(module+ test
  (test-equal (term (sd/a x ())) (term x))
  (test-equal (term (sd/a x ((y) (z) (x)))) (term (K 2 0)))
  (test-equal (term (sd/a ((lambda (x) x) (lambda (y) y)) ()))
              (term ((lambda () (K 0 0)) (lambda () (K 0 0)))))
  (test-equal (term (sd/a (lambda (x) (x (lambda (y) y))) ()))
              (term (lambda () ((K 0 0) (lambda () (K 0 0))))))
  (test-equal (term (sd/a (lambda (z x) (x (lambda (y) z))) ()))
              (term (lambda () ((K 0 1) (lambda () (K 1 0)))))))

(define-metafunction SD
  sd/a : any ((x ...) ...) -> any
  [(sd/a x ((x_1 ...) ... (x_0 ... x x_2 ...) (x_3 ...) ...))
   ; bound variable
   (K n_rib n_pos)
   (where n_rib ,(length (term ((x_1 ...) ...))))
   (where n_pos ,(length (term (x_0 ...))))
   (where #false (in x (x_1 ... ...)))]
  [(sd/a (lambda (x ...) any_1) (any_rest ...))
   (lambda () (sd/a any_1 ((x ...) any_rest ...)))]
  [(sd/a (any_fun any_arg ...) (any_rib ...))
   ((sd/a any_fun (any_rib ...)) (sd/a any_arg (any_rib ...)) ...)]
  [(sd/a any_1 any)
   ; free variable, constant, etc
   any_1])

2.2.5 Substitution

The last thing we need is substitution, because it is the syntactic equivalent of function application. We define it with any having future extensions in mind.

; (subst ([e x] ...) e_*) substitutes e ... for x ... in e_* (hygienically)

(module+ test
  (test-equal (term (subst ([1 x][2 y]) x)) 1)
  (test-equal (term (subst ([1 x][2 y]) y)) 2)
  (test-equal (term (subst ([1 x][2 y]) z)) (term z))
  (test-equal (term (subst ([1 x][2 y]) (lambda (z w) (x y))))
              (term (lambda (z w) (1 2))))
  (test-equal (term (subst ([1 x][2 y]) (lambda (z w) (lambda (x) (x y)))))
              (term (lambda (z w) (lambda (x) (x 2))))
              #:equiv =α/racket)
  (test-equal (term (subst ((2 x)) ((lambda (x) (1 x)) x)))
              (term ((lambda (x) (1 x)) 2))
              #:equiv =α/racket))

(define-metafunction Lambda
  subst : ((any x) ...) any -> any
  [(subst [(any_1 x_1) ... (any_x x) (any_2 x_2) ...] x) any_x]
  [(subst [(any_1 x_1) ...]  x) x]
  [(subst [(any_1 x_1) ...]  (lambda (x ...) any_body))
   (lambda (x_new ...)
     (subst ((any_1 x_1) ...)
            (subst-raw ((x_new x) ...) any_body)))
   (where  (x_new ...)  ,(variables-not-in (term any_body) (term (x ...))))]
  [(subst [(any_1 x_1) ...]  (any ...)) ((subst [(any_1 x_1) ...]  any) ...)]
  [(subst [(any_1 x_1) ...]  any_*) any_*])

(define-metafunction Lambda
  subst-raw : ((x x) ...) any -> any
  [(subst-raw ((x_n1 x_o1) ... (x_new x) (x_n2 x_o2) ...) x) x_new]
  [(subst-raw ((x_n1 x_o1) ...)  x) x]
  [(subst-raw ((x_n1 x_o1) ...)  (lambda (x ...) any))
   (lambda (x ...) (subst-raw ((x_n1 x_o1) ...)  any))]
  [(subst-raw [(any_1 x_1) ...]  (any ...))
   ((subst-raw [(any_1 x_1) ...]  any) ...)]
  [(subst-raw [(any_1 x_1) ...]  any_*) any_*])

}

2.3 Lab Designing Metafunctions

Goals

— developing meta-functions

— discovering Redex patterns

The following exercises refer to several definitions found in, and exported from, "common.rkt". You may either copy these definitions into your file or add the following require statement to the top of your file:

(require "common.rkt")

Exercises

Exercise 1. Design bv. The metafunction determines the bound variables in a Lambda expression. A variable x is bound in e_Lambda if x occurs in a lambda-parameter list in e_Lambda.

Exercise 2. Design lookup. The metafunction consumes a variable and an environment. It determines the leftmost expression associated with the variable; otherwise it produces #false.
Here is the definition of environment:
(define-extended-language Env Lambda
(e ::= .... natural)
(env ::= ((x e) ...)))
The language extension also adds numbers of the sub-language of expressions.
Before you get started, make sure you can create examples of environments and confirm their well-formedness.

Exercise 3. Develop the metafunction let, which extends the language with a notational shorthand, also known as syntactic sugar.
Once you have this metafunction, you can write expressions such as
(term
  (let ((x (lambda (a b c) a))
        (y (lambda (x) x)))
    (x y y y)))
Like Racket’s let, the function elaborates surface syntax into core syntax:
(term
  ((lambda (x y) (x y y y))
   (lambda (a b c) a)
   (lambda (x) x)))
Since this elaboration happens as the term is constructed, all other metafunctions work as expected on this extended syntax. For example,
(term
(fv
  (let ((x (lambda (a b c) a))
        (y (lambda (x) x)))
    (x y y y))))
or
(term
(bv
  (let ((x (lambda (a b c) a))
        (y (lambda (x) x)))
    (x y y y))))
produces the expected results. What are those?

2.4 Reductions and Semantics

Goals

— extend languages with concepts needed for reduction relations

— developing reduction relations

— defining a semantics

— testing against a language

Note These notes deal with the λβ calculus, specifically its reduction system.

notation

meaning
x

basic notion of reduction, without properties
-->x

one-step reduction, generated from x, compatible with syntactic constructions
-->>x

reduction, generated from -->x, transitive here also reflexive
=x

“calculus”, generated from -->x, symmetric, transitive, reflexive

2.4.1 Contexts, Values

The logical way of generating an equivalence (or reduction) relation over terms uses through inductive inference rules that make the relation compatible with all syntactic constructions.

An alternative and equivalent method is to introduce the notion of a context and to use it to generate the reduction relation (or equivalence) from the notion of reduction:

(require "common.rkt")

(define-extended-language Lambda-calculus Lambda
  (e ::= .... n)
  (n ::= natural)
  (v ::= (lambda (x ...) e))

  ; a context is an expression with one hole in lieu of a sub-expression
  (C ::=
     hole
     (e ... C e ...)
     (lambda (x_!_ ...) C)))

(define Context? (redex-match? Lambda-calculus C))

(module+ test
  (define C1 (term ((lambda (x y) x) hole 1)))
  (define C2 (term ((lambda (x y) hole) 0 1)))
  (test-equal (Context? C1) #true)
  (test-equal (Context? C2) #true))

Filling the hole of context with an expression yields an expression:

(module+ test
  (define e1 (term (in-hole ,C1 1)))
  (define e2 (term (in-hole ,C2 x)))

  (test-equal (in-Lambda/n? e1) #true)
  (test-equal (in-Lambda/n? e2) #true))

What does filling the hole of a context with a context yield?

2.4.2 Reduction Relations

Developing a reduction relation is like developing a function. Work through examples first. A reduction relation does not have to be a function, meaning it may reduce one and the same term to distinct terms.

; the λβ calculus, reductions only
(module+ test
  ; does the one-step reduction reduce both β redexes?
  (test--> -->β
           #:equiv =α/racket
           (term ((lambda (x) ((lambda (y) y) x)) z))
           (term ((lambda (x) x) z))
           (term ((lambda (y) y) z)))

  ; does the full reduction relation reduce all redexes?
  (test-->> -->β
            (term ((lambda (x y) (x 1 y 2))
                   (lambda (a b c) a)
                   3))
            1))

(define -->β
  (reduction-relation
   Lambda-calculus
   (--> (in-hole C ((lambda (x_1 ..._n) e) e_1 ..._n))
        (in-hole C (subst ([e_1 x_1] ...) e)))))

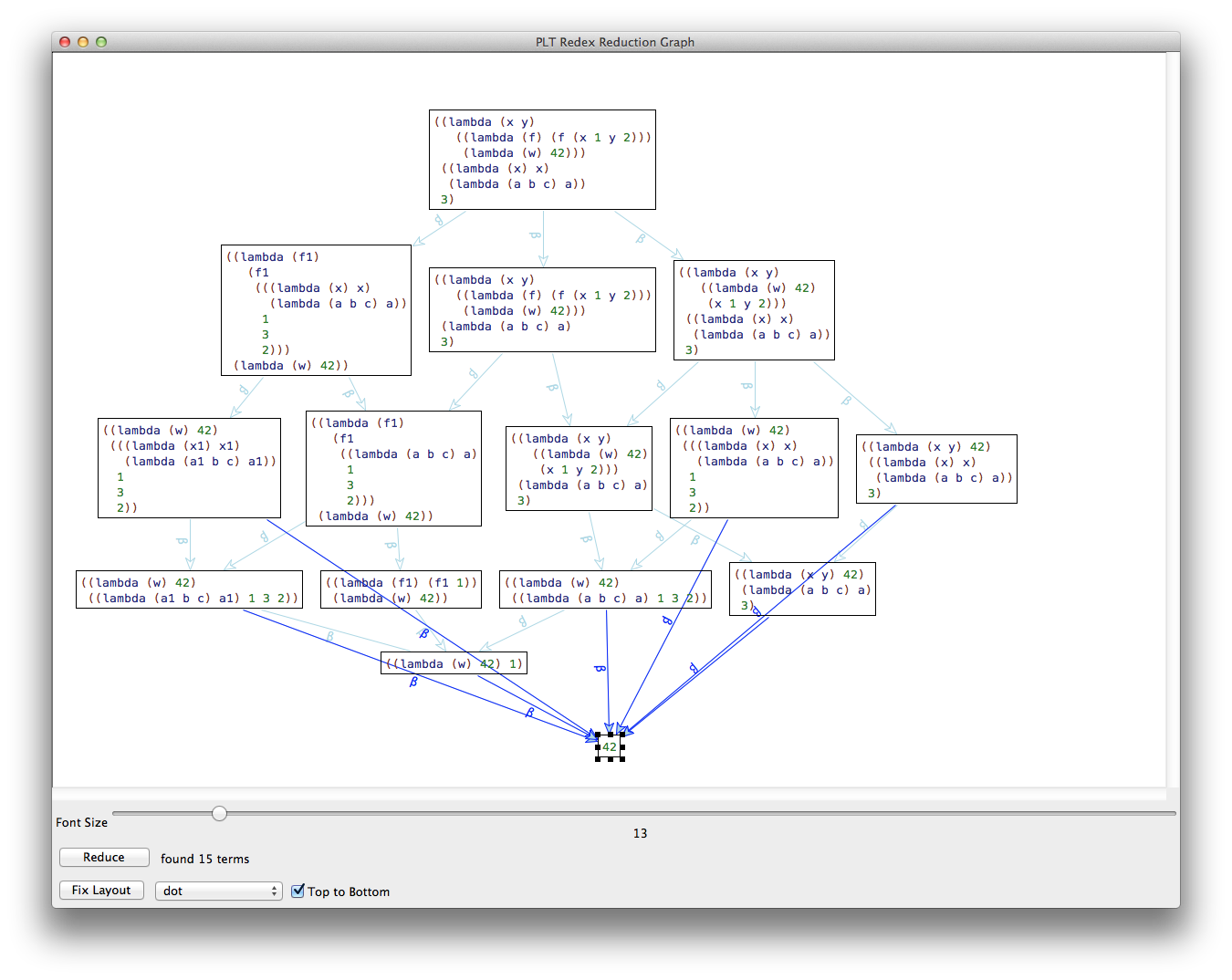
With traces we can visualize reduction graphs:

(traces -->β
        (term ((lambda (x y)
                 ((lambda (f) (f (x 1 y 2)))
                  (lambda (w) 42)))
               ((lambda (x) x) (lambda (a b c) a))
               3)))

Defining the call-by-value calculus requires just a small change to the reduction rule:

(define -->βv
  (reduction-relation
   Lambda-calculus
   (--> (in-hole C ((lambda (x_1 ..._n) e) v_1 ..._n))
        (in-hole C (subst ([v_1 x_1] ...) e)))))

Let’s compare traces for the same term. You do get the same result but significantly fewer intermediate terms. Why?

2.4.3 Semantics

First we need a standard reduction relation. The key is to define the path to the leftmost-outermost redex, which can again be done via contexts. Here are the relevant definitions for the by-value reduction relation:

(define-extended-language Standard Lambda-calculus
  (v ::= n (lambda (x ...) e))
  (E ::=
     hole
     (v ... E e ...)))

(module+ test
  (define t0
    (term
     ((lambda (x y) (x y))
      ((lambda (x) x) (lambda (x) x))
      ((lambda (x) x) 5))))
  (define t0-one-step
    (term
     ((lambda (x y) (x y))
      (lambda (x) x)
      ((lambda (x) x) 5))))

  ; yields only one term, leftmost-outermost
  (test--> s->βv t0 t0-one-step)
  ; but the transitive closure drives it to 5
  (test-->> s->βv t0 5))

(define s->βv
  (reduction-relation
   Standard
   (--> (in-hole E ((lambda (x_1 ..._n) e) v_1 ..._n))
        (in-hole E (subst ((v_1 x_1) ...) e)))))

Note the tests-first development of the relation.

Now we can define the semantics function:

(module+ test
  (test-equal (term (eval-value ,t0)) 5)
  (test-equal (term (eval-value ,t0-one-step)) 5)

  (define t1
    (term ((lambda (x) x) (lambda (x) x))))
  (test-equal (lambda? t1) #true)
  (test-equal (redex-match? Standard e t1) #true)
  (test-equal (term (eval-value ,t1)) 'closure))

(define-metafunction Standard
  eval-value : e -> v or closure
  [(eval-value e) any_1 (where any_1 (run-value e))])

(define-metafunction Standard
  run-value : e -> v or closure
  [(run-value n) n]
  [(run-value v) closure]
  [(run-value e)
   (run-value e_again)
   ; (v) means that we expect s->βv to be a function
   (where (e_again) ,(apply-reduction-relation s->βv (term e)))])

The key is the stepper-loop, which applies the Racket function apply-reduction-relation repeatedly until it yields a value.

2.4.4 What are Models

Good models of programming languages are like Newtonian models of how you drive a car. As long as your speed is within a reasonable interval, the model accurately predicts how your car behaves. Similarly, as long as your terms are within a reasonable subset (the model’s language), the evaluator of the model and the evaluator of the language ought to agree.

For Racket you set up an evaluator for the language like this:

(define-namespace-anchor A)
(define N (namespace-anchor->namespace A))
; Lambda.e -> Number or 'closure or exn
(define (racket-evaluator t0)
  (define result
    (with-handlers ((exn:fail? values))
      (eval t0 N)))
  (cond
    [(number? result) result]
    [(procedure? result) (term closure)]
    [else (make-exn "hello world" (current-continuation-marks))]))

The details don’t matter.

So the theorem is this:

(define-metafunction Standard
  theorem:racket=eval-value : e -> boolean
  [(theorem:racket=eval-value e)
   ,(letrec ([rr (racket-evaluator (term e))]
             [vr (term (run-value e))])
      (cond
        [(and (exn? rr) (eq? (term stuck) vr))
         #true]
        [(exn? rr) #false]
        [(eq? (term stuck) vr) #false]
        [else (equal? vr rr)]))])

We formulate it as a meta-function and test it on some terms:

(module+ test
  (test-equal (term (racket=eval-value ,t0)) #true)
  (test-equal (term (racket=eval-value ,t0-one-step)) #true)
  (test-equal (term (racket=eval-value ,t1)) #true))

The real test comes with random testing:

(redex-check Standard e (term (theorem:racket=eval-value e)))

And now it’s time to discover.

2.5 Lab Designing Reductions

Goals

— developing reductions

— semantics

(require "common.rkt")

Also require "close.rkt" for the fv function.

You also want to copy the following definitions into your drracket:

(define-extended-language Lambda-η Lambda
  (e ::= .... n)
  (n ::= natural)
  (C ::=
     hole
     (e ... C e ...)
     (lambda (x_!_ ...) C))
  (v ::=
     n
     (lambda (x ...) e)))

(define -->β
  (reduction-relation
   Lambda-η
   (--> (in-hole C ((lambda (x_1 ..._n) e) e_1 ..._n))
        (in-hole C (subst ([e_1 x_1] ...) e))
        β)))

(define lambda? (redex-match? Lambda-calculus e))

Consider equipping the one-step reduction relation with tests.

Exercises

Exercise 4. Develop a βη reduction relation for Lambda-η.
Find a term that contains both a β- and an η-redex. Formulate a Redex test that validates this claim. Also use trace to graphically validate the claim.
Develop the β and βη standard reduction relations. Hint Look up extend-reduction-relation to save some work.
Use the standard reduction relations to formulate a semantics for both variants. The above test case, reformulated for the standard reduction, must fail. Why? Note The semantics for βη requires some experimentation. Justify your non-standard definition of the run function.
The βη semantics is equivalent to the β variant. Formulate this theorem as a metafunction. Use redex-check to test your theorem.
Note Why does it make no sense to add η to this system?

Exercise 5. Extend the by-value language with an addition operator.
Equip both the βv reduction system and the βv standard reduction with rules that assign addition the usual semantics. Finally define a semantics functions for this language.
Hint Your rules need to escape to Racket and use its addition operator.

2.6 Types and Property Testing

Goals

— typed languages

— developing type judgments

— subject reduction

2.6.1 Types

Here is a typed variant of the Lambda language:

(define-language TLambda
  (e ::=
     n
     +
     x
     (lambda ((x_!_ t) ...) e)
     (e e ...))
  (t ::=
     int
     (t ... -> t))
  (x ::= variable-not-otherwise-mentioned))

(define lambda? (redex-match? TLambda e))

(define e1
  (term (lambda ((x int) (f (int -> int))) (+ (f (f x)) (f x)))))
(define e2
  (term (lambda ((x int) (f ((int -> int) -> int))) (f x))))
(define e3
  (term (lambda ((x int) (x (int -> int))) x)))

(module+ test
  (test-equal (lambda? e1) #true)
  (test-equal (lambda? e2) #true)
  (test-equal (in-TLambda? e3) #false))

2.6.2 Developing Type Judgments

Like metafunctions and reduction relations, type judgments are developed by working out examples, formulating tests, and then articulating the judgment rules:

; (⊢ Γ e t) – the usual type judgment for an LC language

(define-extended-language TLambda-tc TLambda
  (Γ ::= ((x t) ...)))

(module+ test
  (test-equal (judgment-holds (⊢ () ,e1 (int (int -> int) -> int))) #true)
  (test-equal (judgment-holds (⊢ () ,e2 t)) #false)
  (displayln  (judgment-holds (⊢ () ,e1 t) t))
  (displayln  (judgment-holds (⊢ () ,e2 t) t)))

(define-judgment-form TLambda-tc
  #:mode (⊢ I I O)
  #:contract (⊢ Γ e t)
  [----------------------- "number"
   (⊢ Γ n int)]

  [----------------------- "+"
   (⊢ Γ + (int int -> int))]

  [----------------------- "variable"
   (⊢ Γ x (lookup Γ x))]

  [(⊢ (extend Γ (x_1 t_1) ...) e t)
   ------------------------------------------------- "lambda"
   (⊢ Γ (lambda ((x_1 t_1) ...) e) (t_1 ... -> t))]

  [(⊢ Γ e_1 (t_2 ... -> t))
   (⊢ Γ e_2 t_2) ...
   ------------------------------------------------- "application"
   (⊢ Γ (e_1 e_2 ...) t)])

Here are the necessary auxiliary functions:

; (extend Γ (x t) ...) add (x t) to Γ so that x is found before other x-s
(module+ test
  (test-equal (term (extend () (x int))) (term ((x int)))))

(define-metafunction TLambda-tc
  extend : Γ (x t) ... -> Γ
  [(extend ((x_Γ t_Γ) ...) (x t) ...) ((x t) ...(x_Γ t_Γ) ...)])

; (lookup Γ x) retrieves x's type from Γ
(module+ test
  (test-equal (term (lookup ((x int) (x (int -> int)) (y int)) x)) (term int))
  (test-equal (term (lookup ((x int) (x (int -> int)) (y int)) y)) (term int)))

(define-metafunction TLambda-tc
  lookup : Γ x -> t
  [(lookup ((x_1 t_1) ... (x t) (x_2 t_2) ...) x)
   t
   (side-condition (not (member (term x) (term (x_1 ...)))))]
  [(lookup any_1 any_2) ,(error 'lookup "not found: ~e" (term x))])

2.6.3 Subjection Reduction

Let’s say we define a truly broken (standard) reduction relation for TLambda:

(define ->
  (reduction-relation
   TLambda
   #:domain e
   (--> e (lambda ((x int)) x))))

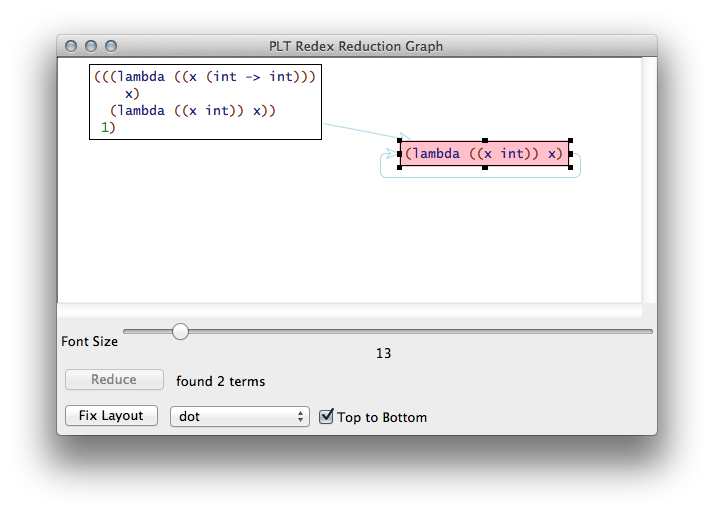
With trace, we can quickly see that paths in almost any term’s reduction graph do not preserve types:

(traces ->
(term (((lambda ((x (int -> int))) x) (lambda ((x int)) x)) 1))
#:pred (lambda (e) (judgment-holds (⊢ () ,e int))))

The #:pred keyword argument supplies a Racket function that judges whether the intermediate expression type checks, using our type judgment from above.

For simple “type systems,” redex-check can be used to test a true subject reduction statement:

(redex-check TLambda
             e
             (implies (judgment-holds (⊢ () e int))
                      (judgment-holds (⊢ () (eval-value e) int)))
             #:attempts 3)

2.7 Lab Type Checking

Goals

— subject reduction testing with trace

— typing judgments

(require "common.rkt")

In addition to "common.rkt", you also want to require "tc-common.rkt" for this lab. Furthermore, if you copy code from Types and Property Testing, make sure to copy the tests and to adapt the tests as you develop the machines.

Exercises

Exercise 6. Develop a reduction system for which the trace expression from the lecture preserves types
(module+ test
  (traces ->
          (term (((lambda ((x (int -> int))) x) (lambda ((x int)) x)) 1))
          #:pred (lambda (e)
                   (judgment-holds (⊢ () ,e int)))))

Exercise 7. Extend TLambda with syntax for the following:
additional numeric operators, say, multiplication, subtraction, and division;
let expressions;
Boolean constants plus strict and and or operators as well as a branching construct;
lists, specifically constructors and selectors (de-constructors);
explicitly recursive function definitions.
Completing the above list is an ambitious undertaking, but do try to complete at least two or three of these tasks.

2.8 Imperative Extensions

Goals

— revise the language for assignment statements

— a standard reduction system for expression-store tuples

— revise the language for raising exceptions

— a general reduction system for exceptions

2.8.1 Variable Assignment

Let’s add variable assignments to our language:

(define-extended-language Assignments Lambda
(e ::= .... n + (void) (set! x e))
(n ::= natural))

This makes it like Racket, Scheme and Lisp, but unlike ML where you can mutate only data structure (one-slot records in SML and slots in arbitrary records in OCaml.

For writing programs in this world, you also want blocks and local declarations. We add a task-specific let expression:

; (let ((x_1 x_2) ...) e_1 e_2) binds the current value of x_2 to x_1,
; evaluates e_1, throws away its value, and finally evaluates e_2
(define-metafunction Assignments
  let : ((x e) ...) e e -> e
  [(let ([x_lhs e_rhs] ...) e_1 e_2)
   ((lambda (x_lhs ...)
      ((lambda (x_dummy) e_2) e_1))
    e_rhs ...)
   (where (x_dummy) ,(variables-not-in (term (e_1 e_2)) '(dummy)))])

Here are some sample programs:

(define e1
  (term
   (lambda (x)
     (lambda (y)
       (let ([tmp x])
         (set! x (+ y 1))
         tmp)))))

(define p-1 (term ((,e1 1) 2)))

(define e2
  (term
   ((lambda (x)
      (let ([tmp x])
        (set! x y)
        tmp))
    (let ([tmp-z z])
      (set! z (+ z 1))
      (let ([tmp-y y])
        (set! y tmp-z)
        tmp-y)))))

(define p-2
  (term ((lambda (y) ((lambda (z) ,e2) 1)) 2)))

How do they behave?

For a standard reduction relation, we need both evaluation contexts and a table that keeps track of the current value of variables:

(define-extended-language Assignments-s Assignments
  (E ::= hole (v ... E e ...) (set! x E))
  (σ ::= ((x v) ...))
  (v ::= n + (void) (lambda (x ...) e)))

; (extend σ x v) adds (x v) to σ
(define-metafunction Assignments-s
  extend : σ (x ...) (any ...) -> σ
  [(extend ((x any) ...) (x_1 ...) (any_1 ...)) ((x_1 any_1) ... (x any) ...)])

; —————————————————————————–
; (lookup Γ x) retrieves x's type from Γ
(define-metafunction Assignments-s
  lookup : any x -> any
  [(lookup ((x_1 any_1) ... (x any_t) (x_2 any_2) ...) x)
   any_t
   (side-condition (not (member (term x) (term (x_1 ...)))))]
  [(lookup any_1 any_2)
   ,(error 'lookup "not found: ~e in: ~e" (term x) (term any_2))])

Extending this table and looking up values in it, is a routine matter by now.

Here is the standard reduction relation:

(define s->βs
  (reduction-relation
   Assignments-s
   #:domain (e σ)
   (--> [(in-hole E x) σ]
        [(in-hole E (lookup σ x)) σ])
   (--> [(in-hole E (set! x v)) σ]
        [(in-hole E (void)) (extend σ (x) (v))])
   (--> [(in-hole E (+ n_1 n_2)) σ]
        [(in-hole E ,(+ (term n_1) (term n_2))) σ])
   (--> [(in-hole E ((lambda (x ..._n) e) v ..._n)) σ]
        [(in-hole E e) (extend σ (x_new ...) (v ...))]
        (where (x_new ...) ,(variables-not-in (term σ) (term (x ...)))))))

The question is what the corresponding calculus looks like. See Lab Contexts and Stores.

This use of the standard reduction relation is common because most researchers do not need the calculus. Instead they define such a relation and consider it a semantics.

The semantics is a function, however, that maps programs to the final answers and possibly extracts pieces from the store.

(module+ test
  (test-equal (term (eval-assignments ,p-1)) 1)
  (test-equal (term (eval-assignments ,p-2)) 2)
  (test-equal (term (eval-assignments ,p-c)) (term closure)))

(define-metafunction Assignments-s
  eval-assignments : e -> v or closure
  [(eval-assignments e) (run-assignments (e ()))])

(define-metafunction Assignments-s
  run-assignments : (e σ) -> v or closure
  [(run-assignments (n σ)) n]
  [(run-assignments (v σ)) closure]
  [(run-assignments any_1)
   (run-assignments any_again)
   (where (any_again) ,(apply-reduction-relation s->βs (term any_1)))]
  [(run-assignments any) stuck])

2.8.2 Raising Exceptions

When non-local control operators come such as ML’s exceptions come into play, reductions become (evaluation-) context-sensitive.

Here is a language with a simple construct for raising exceptions:

(define-extended-language Exceptions Lambda
(e ::= .... n + (raise e))
(n ::= integer))

History This form of exception was actually introduced into Lisp as the catch and throw combination (contrary to some statements in Turing-award announcements).

Try to figure out what these expressions ought to compute:

(define c1
  (term
   ((lambda (x)
      (+ 1 (raise (+ 1 x))))
    0)))

(define c2
  (term
   (lambda (y)
     ((lambda (x)
        (+ 1 (raise (+ (raise -1) x))))
      0))))

A calculus of exceptions needs both arbitrary term contexts and evaluation contexts:

(define-extended-language Exceptions-s Exceptions
  (C ::= hole (e ... C e ...) (lambda (x ...) C) (raise C))
  (E ::= hole (v ... E e ...) (raise E))
  (v ::= n + (lambda (x ...) e)))

The key insight is that an exception-raising construct erases any surrounding evaluation context, regardless of where it shows up:

(module+ test
  (test-->> ->βc c1 (term (raise 1)))
  (test-->> ->βc c2 (term (lambda (y) (raise -1)))))

(define ->βc
  (reduction-relation
   Exceptions-s
   (--> (in-hole C (in-hole E (raise v)))
        (in-hole C (raise v))
        (where #false ,(equal? (term E) (term hole)))
        ζ)
   (--> (in-hole C (+ n_1 n_2))
        (in-hole C ,(+ (term n_1) (term n_2)))
        +)
   (--> (in-hole C ((lambda (x_1 ..._n) e) v_1 ..._n))
        (in-hole C (subst ([v_1 x_1] ...) e))
        β_v)))

The question is what a standard reduction relation for such a calculus looks like. See Lab Contexts and Stores.

2.9 Lab Contexts and Stores

Goals

— develop a general reduction system for Lambda with assignments

— develop a standard reduction system for Lambda with exceptions

(require "common.rkt")

Also require "extend-lookup.rkt". Feel free to copy code from Imperative Extensions but make sure to add tests.

Exercises

The exercises this morning are puzzles. Try your hands on them, but when you feel stuck, don’t hesitate to request help.

Exercise 8. Develop a reduction relation for assignment statements. Add a letrec syntax to the language like this:
(define-extended-language ImperativeCalculus Assignments
(e ::= .... (letrec ((x v) ...) e)))
A letrec mutually recursively binds the variables x ... to the values v ... and in e. The addition of letrec internalizes the store into the language. Adapt the existing relations.
Develop terms that one-step reduce in several different directions via reductions that model assignment and/or variable derefences. Use trace graphs to demonstrate the idea.
Note This calculus has naturally separated mini-heaps, but your system must extrude the scope of these heaps on occasion (when values are returned) and merge them.

Exercise 9. Develop a standard reduction system and a semantics for exceptions.
Note You need to use evaluation contexts for two distinct purposes.

Exercise 10. Develop a semantics of for a control operator such as callcc.
Request Check with one of us before you embark on this project. We want to make sure that (1) the operator isn’t too difficult and (2) not to easy to implement. We are also available for hints.

2.10 Abstract Machines

Goals

— why these three machines: CC machine, CK machine, CEK machine

— theorems connecting the machines, theorems for debugging

— equivalence theorems

2.10.1 CC Machine

Observation β and β_v redexes often take place repeatedly in the same evaluation context. On occasion they just add more layers (inside the hole) to the evaluation context. Let’s separate the in-focus expression from the evaluation context. Historically the two have been called control string (C) and control context (C).

(define-extended-language Lambda/v Lambda
  (e ::= .... n +)
  (n ::= integer)
  (v ::= n + (lambda (x ...) e)))

(define vv? (redex-match? Lambda/v e))

(define e0
  (term ((lambda (x) x) 0)))

(define e1
  (term ((lambda (x y) x) 1 2)))

(module+ test
  (test-equal (vv? e1) #true)
  (test-equal (vv? e0) #true))

; —————————————————————————–
; the CC machine: keep contexts and expression-in-focus apart

(define-extended-language CC Lambda/v
  (E ::=
     hole
     ; Note right to left evaluation of application
     (e ... E v ...)))

(module+ test
  (test-->> -->cc (term [,e0 hole]) (term [0 hole]))
  (test-->> -->cc (term [,e1 hole]) (term [1 hole])))

(define -->cc
  (reduction-relation
   CC
   #:domain (e E)
   (--> [(lambda (x ..._n) e)
         (in-hole E (hole v ..._n))]
        [(subst ([v x] ...) e) E]
        CC-β_v)
   (--> [+
         (in-hole E (hole n_1 n_2))]
        [,(+ (term n_1) (term n_2)) E]
        CC-+)
   (--> [(e_1 ...) E]
        [e_last (in-hole E (e_1others ... hole))]
        (where (e_1others ... e_last) (e_1 ...))
        CC-push)
   (--> [v      (in-hole E (e ... hole v_1 ...))]
        [e_last (in-hole E (e_prefix ... hole v v_1 ...))]
        (where (e_prefix ... e_last) (e ...))
        CC-switch)))

(module+ test
  (test-equal (term (eval-cc ,e0)) 0)
  (test-equal (term (eval-cc ,e1)) 1))

(define-metafunction Lambda/v
  eval-cc : e -> v or closure or stuck
  [(eval-cc e) (run-cc [e hole])])

(define-metafunction CC
  run-cc : (e E) -> v or closure or stuck
  [(run-cc (n hole)) n]
  [(run-cc (v hole)) closure]
  [(run-cc any_1)
   (run-cc (e_again E_again))
   (where ((e_again E_again)) ,(apply-reduction-relation -->cc (term any_1)))]
  [(run-cc any) stuck])

2.10.2 The CK Machine

Observation The evaluation context of the CC machine behaves exactly like a control stack. Let’s represent it as such.

General Idea The general idea is to show how valuable it is to reconsider data representations in PL, and how easy it is to do so in Redex.

(define-extended-language CK Lambda/v
  ; Note encode context as stack (left is top)
  (k ::= ((app [v ...] [e ...]) ...)))

(module+ test
  (test-->> -->ck (term [,e0 ()]) (term [0 ()]))
  (test-->> -->ck (term [,e1 ()]) (term [1 ()])))

(define -->ck
  (reduction-relation
   CK
   #:domain (e k)
   (--> [(lambda (x ..._n) e)
         ((app [v ..._n] []) (app any_v any_e) ...)]
        [(subst ([v x] ...) e)
         ((app any_v any_e) ...)]
        CK-β_v)
   (--> [+ ((app [n_1 n_2] []) (app any_v any_e) ...)]
        [,(+ (term n_1) (term n_2)) ((app any_v any_e) ...)]
        CK-+)
   (--> [(e_1 ...) (any_k ...)]
        [e_last ((app () (e_1others ...)) any_k ...)]
        (where (e_1others ... e_last) (e_1 ...))
        CK-push)
   (--> [v ((app (v_1 ...) (e ...)) any_k ...)]
        [e_last ((app (v v_1 ...) (e_prefix ...)) any_k ...)]
        (where (e_prefix ... e_last) (e ...))
        CK-switch)))

(module+ test
  (test-equal (term (eval-ck ,e0)) 0)
  (test-equal (term (eval-ck ,e1)) 1))

(define-metafunction Lambda/v
  eval-ck : e -> v or closure or stuck
  [(eval-ck e) (run-ck [e ()])])

(define-metafunction CK
  run-ck : (e k) -> v or closure or stuck
  [(run-ck (n ())) n]
  [(run-ck (v ())) closure]
  [(run-ck any_1)
   (run-ck (e_again k_again))
   (where ((e_again k_again)) ,(apply-reduction-relation -->ck (term any_1)))]
  [(run-ck any) stuck])

2.10.3 The CC-CK Theorem

The two machines define the same evaluation function. Let’s formulate this as a theorem and redex-check it.

Note When I prepared these notes, I found two mistakes in my machines.

(module+ test
  ; theorem:eval-ck=eval-cc
  (test-equal (term (theorem:eval-ck=eval-cc ,e0)) #true)
  (test-equal (term (theorem:eval-ck=eval-cc ,e1)) #true)

  ; NEXT: CEK vs CK
  (redex-check Lambda e (term (theorem:eval-ck=eval-cc e))
               #:attempts 24
               #:prepare (close-all-fv vv?)))

(define-metafunction Lambda/v
  theorem:eval-ck=eval-cc : e -> boolean
  [(theorem:eval-ck=eval-cc e)
   ,(equal? (term (eval-cc e)) (term (eval-ck e)))])

2.10.4 The CEK machine

Observation Substitution is an eager operation. It traverses the term kind of like machine does anyway when it searches for a redex. Why not combine the two by delaying substitution until needed? That’s called an environment (E) in the contexts of machines (also see above).

General Idea Universal laziness is not a good idea. But the selective delay of operations—especially when operations can be merged—is a good thing.

(define-extended-language CEK Lambda/v
  (ρ ::= ((x c) ...))
  (c ::= (v ρ))
  (k ::= ((app [c ...] ρ [e ...]) ...)))

(module+ test
  (test-->> -->cek (term [,e0 () ()]) (term [0 () ()]))
  (test-->> -->cek (term [,e1 () ()]) (term [1 () ()])))

(define -->cek
  (reduction-relation
   CEK
   #:domain (e ρ k)
   (--> [x
         ((x_1 c_1) ... (x (v ρ)) (x_2 c_2) ...)
         ((app any_v any_r any_e) ...)]
        [v
         ρ
         ((app any_v any_r any_e) ...)]
        CEK-lookup)
   (--> [(lambda (x ..._n) e)
         (any_c ...)
         ((app [c ..._n] ρ []) (app any_v any_r any_e) ...)]
        [e
         ([x c] ... any_c ...)
         ((app any_v any_r any_e) ...)]
        CEK-β_v)
   (--> [+
         ρ
         ((app [n_1 n_2] []) (app any_v any_r any_e) ...)]
        [,(+ (term n_1) (term n_2))
         ()
         ((app any_v any_r any_e) ...)]
        CEK-+)
   (--> [(e_1 ...)
         ρ
         (any_k ...)]
        [e_last
         ρ
         ((app () ρ (e_1others ...)) any_k ...)]
        (where (e_1others ... e_last) (e_1 ...))
        CEK-push)
   (--> [v
         ρ
         ((app (c_1 ...) ρ_stack (e ...)) any_k ...)]
        [e_last
         ρ_stack
         ((app ((v ρ) c_1 ...) ρ_stack (e_prefix ...)) any_k ...)]
        (where (e_prefix ... e_last) (e ...))
        CEK-switch)))

(module+ test
  (test-equal (term (eval-cek ,e0)) 0)
  (test-equal (term (eval-cek ,e1)) 1))

(define-metafunction Lambda/v
  eval-cek : e -> v or closure or stuck
  [(eval-cek e) (run-cek [e () ()])])

(define-metafunction CEK
  run-cek : (e ρ k) -> v or closure or stuck
  [(run-cek (n ρ ())) n]
  [(run-cek (v ρ ())) closure]
  [(run-cek any_1)
   (run-cek (e_again ρ_again k_again))
   (where ((e_again ρ_again k_again))
          ,(apply-reduction-relation -->cek (term any_1)))]
  [(run-cek any) stuck])

2.10.5 The CEK-CK Theorem

Again, the two machines define the same semantics. Here is the theorem.

(module+ test
  ; theorem:eval-ck=eval-cc
  (test-equal (term (theorem:eval-cek=eval-ck ,e0)) #true)
  (test-equal (term (theorem:eval-cek=eval-ck ,e1)) #true)

  ; NEXT: CEK vs CK
  (redex-check Lambda e (term (theorem:eval-cek=eval-ck e))
               #:attempts 24
               #:prepare (close-all-fv vv?)))

(define-metafunction Lambda/v
  theorem:eval-cek=eval-ck : e -> boolean
  [(theorem:eval-cek=eval-ck e)
   ,(equal? (term (eval-cek e)) (term (eval-ck e)))])

2.11 Lab Machine Transitions

Goals

— develop the CESK machine

(require "common.rkt")

In addition to "common.rkt", you also want to require "close.rkt" for this lab. Furthermore, if you copy code from Abstract Machines, make sure to copy the tests and to adapt the tests as you develop the machines.

Exercises

Exercise 11. Equip the language with assignment statements and void:
(define-extended-language Assignments Lambda
(e ::= .... n + (void) (set! x e))
(n ::= natural))
Start with the CS reduction system and develop the CESK machine, re-tracing the above machine derivation.

2.12 Abstracting Abstract Machines

David Van Horn presented his tutorial on Abstracting Abstract Machines in Redex.

2.13 "common.rkt"

#lang racket

;; basic definitions for the Redex Summer School 2015

(provide

;; Language

Lambda

;; Any -> Boolean

;; is the given value in the expression language?

lambda?

;; x (x ...) -> Boolean

;; (in x (x_1 ...)) determines whether x occurs in x_1 ...

;; Any Any -> Boolean

;; (=α/racket e_1 e_2) determines whether e_1 is α-equivalent to e_2

;; e_1, e_2 are in Lambda or extensions of Lambda that

;; do not introduce binding constructs beyond lambda

=α/racket

;; ((Lambda x) ...) Lambda -> Lambda

;; (subs ((e_1 x_1) ...) e) substitures e_1 for x_1 ... in e

;; e_1, ... e are in Lambda or extensions of Lambda that

;; do not introduce binding constructs beyond lambda

subst)

;; -----------------------------------------------------------------------------

(require redex)

(define-language Lambda

(e ::=

(lambda (x_!_ ...) e)

(e e ...))

(x ::= variable-not-otherwise-mentioned))

(define lambda? (redex-match? Lambda e))

(module+ test

(define e1 (term y))

(define e2 (term (lambda (y) y)))

(define e3 (term (lambda (x y) y)))

(define e4 (term (,e2 e3)))

(test-equal (lambda? e1) #true)

(test-equal (lambda? e2) #true)

(test-equal (lambda? e3) #true)

(test-equal (lambda? e4) #true)

(define eb1 (term (lambda (x x) y)))

(define eb2 (term (lambda (x y) 3)))

(test-equal (lambda? eb1) #false)

(test-equal (lambda? eb2) #false))

;; -----------------------------------------------------------------------------

;; (in x x_1 ...) is x a member of (x_1 ...)?

(module+ test

(test-equal (term (in x (y z x y z))) #true)

(test-equal (term (in x ())) #false)

(test-equal (term (in x (y z w))) #false))

(define-metafunction Lambda

in : x (x ...) -> boolean

[(in x (x_1 ... x x_2 ...)) #true]

[(in x (x_1 ...)) #false])

;; -----------------------------------------------------------------------------

;; (=α e_1 e_2) determines whether e_1 and e_2 are α equivalent

(module+ test

(test-equal (term (=α (lambda (x) x) (lambda (y) y))) #true)

(test-equal (term (=α (lambda (x) (x 1)) (lambda (y) (y 1)))) #true)

(test-equal (term (=α (lambda (x) x) (lambda (y) z))) #false))

(define-metafunction Lambda

=α : any any -> boolean

[(=α any_1 any_2) ,(equal? (term (sd any_1)) (term (sd any_2)))])

;; a Racket definition for use in Racket positions

(define (=α/racket x y) (term (=α ,x ,y)))

;; (sd e) computes the static distance version of e

(define-extended-language SD Lambda

(e ::= .... (K n))

(n ::= natural))

(define SD? (redex-match? SD e))

(module+ test

(define sd1 (term (K 1)))

(define sd2 (term 1))

(test-equal (SD? sd1) #true))

(define-metafunction SD

sd : any -> any

[(sd any_1) (sd/a any_1 ())])

(module+ test

(test-equal (term (sd/a x ())) (term x))

(test-equal (term (sd/a x ((y) (z) (x)))) (term (K 2 0)))

(test-equal (term (sd/a ((lambda (x) x) (lambda (y) y)) ()))

(term ((lambda () (K 0 0)) (lambda () (K 0 0)))))

(test-equal (term (sd/a (lambda (x) (x (lambda (y) y))) ()))

(term (lambda () ((K 0 0) (lambda () (K 0 0))))))

(test-equal (term (sd/a (lambda (z x) (x (lambda (y) z))) ()))

(term (lambda () ((K 0 1) (lambda () (K 1 0)))))))

(define-metafunction SD

sd/a : any ((x ...) ...) -> any

[(sd/a x ((x_1 ...) ... (x_0 ... x x_2 ...) (x_3 ...) ...))

;; bound variable

(K n_rib n_pos)

(where n_rib ,(length (term ((x_1 ...) ...))))

(where n_pos ,(length (term (x_0 ...))))

(where #false (in x (x_1 ... ...)))]

[(sd/a (lambda (x ...) any_1) (any_rest ...))

(lambda () (sd/a any_1 ((x ...) any_rest ...)))]

[(sd/a (any_fun any_arg ...) (any_rib ...))

((sd/a any_fun (any_rib ...)) (sd/a any_arg (any_rib ...)) ...)]

[(sd/a any_1 any)

;; free variable, constant, etc

any_1])

;; -----------------------------------------------------------------------------

;; (subst ([e x] ...) e_*) substitutes e ... for x ... in e_* (hygienically)

(module+ test

(test-equal (term (subst ([1 x][2 y]) x)) 1)

(test-equal (term (subst ([1 x][2 y]) y)) 2)

(test-equal (term (subst ([1 x][2 y]) z)) (term z))

(test-equal (term (subst ([1 x][2 y]) (lambda (z w) (x y))))

(term (lambda (z w) (1 2))))

(test-equal (term (subst ([1 x][2 y]) (lambda (z w) (lambda (x) (x y)))))

(term (lambda (z w) (lambda (x) (x 2))))

#:equiv =α/racket)

(test-equal (term (subst ((2 x)) ((lambda (x) (1 x)) x)))

(term ((lambda (x) (1 x)) 2))

#:equiv =α/racket)

(test-equal (term (subst (((lambda (x) y) x)) (lambda (y) x)))

(term (lambda (y1) (lambda (x) y)))

#:equiv =α/racket))

(define-metafunction Lambda

subst : ((any x) ...) any -> any

[(subst [(any_1 x_1) ... (any_x x) (any_2 x_2) ...] x) any_x]

[(subst [(any_1 x_1) ... ] x) x]

[(subst [(any_1 x_1) ... ] (lambda (x ...) any_body))

(lambda (x_new ...)

(subst ((any_1 x_1) ...)

(subst-raw ((x_new x) ...) any_body)))

(where (x_new ...) ,(variables-not-in (term (any_body any_1 ...)) (term (x ...)))) ]

[(subst [(any_1 x_1) ... ] (any ...)) ((subst [(any_1 x_1) ... ] any) ...)]

[(subst [(any_1 x_1) ... ] any_*) any_*])

(define-metafunction Lambda

subst-raw : ((x x) ...) any -> any

[(subst-raw ((x_n1 x_o1) ... (x_new x) (x_n2 x_o2) ...) x) x_new]

[(subst-raw ((x_n1 x_o1) ... ) x) x]

[(subst-raw ((x_n1 x_o1) ... ) (lambda (x ...) any))

(lambda (x ...) (subst-raw ((x_n1 x_o1) ... ) any))]

[(subst-raw [(any_1 x_1) ... ] (any ...))

((subst-raw [(any_1 x_1) ... ] any) ...)]

[(subst-raw [(any_1 x_1) ... ] any_*) any_*])

;; -----------------------------------------------------------------------------

(module+ test

(test-results))

2.14 "close.rkt"

#lang racket

;; a function that can close over the free variables of an expression

(provide

;; RACKET

;; [Any-> Boolean: valid expression] ->

;; [Lambda.e #:init [i \x.x] -> Lambda.e]

;; ((close-over-fv-with lambda?) e) closes over all free variables in

;; a Lambda term (or sublanguage w/ no new binding constructs) by

;; binding them to (term (lambda (x) x))

;; ((close-over-fv-with lambda?) e #:init i)

;; like above but binds free vars to i

close-over-fv-with

;; any -> (x ...)

;; computes free variables of given term

fv)

(require redex "common.rkt")

;; -------------------------------------------------------

(module+ test

;; show two dozen terms

(redex-check Lambda e #;displayln (term e)

#:attempts 12

#:prepare (close-over-fv-with lambda?))

;; see 0, can't work

(redex-check Lambda e #;displayln (term e)

#:attempts 12

#:prepare (λ (x) ((close-over-fv-with lambda?) x #:init 0))))

(define ((close-over-fv-with lambda?) e #:init (i (term (lambda (x) x))))

;; this is to work around a bug in redex-check; doesn't always work

(if (lambda? e) (term (close ,e ,i)) i))

(define-metafunction Lambda

close : any any -> any

[(close any_1 any_2)

(let ([x any_2] ...) any_1)

(where (x ...) (unique (fv any_1)))])

(define-metafunction Lambda

;; let : ((x e) ...) e -> e but e plus hole

let : ((x any) ...) any -> any

[(let ([x_lhs any_rhs] ...) any_body)

((lambda (x_lhs ...) any_body) any_rhs ...)])

(define-metafunction Lambda

unique : (x ...) -> (x ...)

[(unique ()) ()]

[(unique (x_1 x_2 ...))

(unique (x_2 ...))

(where #true (in x_1 (x_2 ...)))]

[(unique (x_1 x_2 ...))

(x_1 x_3 ...)

(where (x_3 ...) (unique (x_2 ...)))])

;; -----------------------------------------------------------------------------

(module+ test

(test-equal (term (fv x)) (term (x)))

(test-equal (term (fv (lambda (x) x))) (term ()))

(test-equal (term (fv (lambda (x) (y z x)))) (term (y z))))

(define-metafunction Lambda

fv : any -> (x ...)

[(fv x) (x)]

[(fv (lambda (x ...) any_body))

(subtract (x_e ...) x ...)

(where (x_e ...) (fv any_body))]

[(fv (any_f any_a ...))

(x_f ... x_a ... ...)

(where (x_f ...) (fv any_f))

(where ((x_a ...) ...) ((fv any_a) ...))]

[(fv any) ()])

;; -----------------------------------------------------------------------------

;; (subtract (x ...) x_1 ...) removes x_1 ... from (x ...)

(module+ test

(test-equal (term (subtract (x y z x) x z)) (term (y))))

(define-metafunction Lambda

subtract : (x ...) x ... -> (x ...)

[(subtract (x ...)) (x ...)]

[(subtract (x ...) x_1 x_2 ...)

(subtract (subtract1 (x ...) x_1) x_2 ...)])

(module+ test

(test-equal (term (subtract1 (x y z x) x)) (term (y z))))

(define-metafunction Lambda

subtract1 : (x ...) x -> (x ...)

[(subtract1 (x_1 ... x x_2 ...) x)

(x_1 ... x_2new ...)

(where (x_2new ...) (subtract1 (x_2 ...) x))

(where #false (in x (x_1 ...)))]

[(subtract1 (x ...) x_1) (x ...)])

2.15 "tc-common.rkt"

#lang racket

(provide

;; language

TLambda-tc

;; (extend Γ (x t) ...) add (x t) to Γ so that x is found before other x-s

extend

;; (lookup Γ x) retrieves x's type from Γ

lookup)

(require redex)

;; -----------------------------------------------------------------------------

(define-language TLambda-tc

(e ::= n + x (lambda ((x_!_ t) ...) e) (e e ...))

(n ::= natural)

(t ::= int (t ... -> t))

(Γ ::= ((x t) ...))

(x ::= variable-not-otherwise-mentioned))

(define tlambda? (redex-match? TLambda-tc e))

;; -----------------------------------------------------------------------------

;; (extend Γ (x t) ...) add (x t) to Γ so that x is found before other x-s

(module+ test

(test-equal (term (extend () (x int))) (term ((x int)))))

(define-metafunction TLambda-tc

extend : Γ (x any) ... -> any

[(extend ((x_Γ any_Γ) ...) (x any) ...) ((x any) ...(x_Γ any_Γ) ...)])

;; -----------------------------------------------------------------------------

;; (lookup Γ x) retrieves x's type from Γ

(module+ test

(test-equal (term (lookup ((x int) (x (int -> int)) (y int)) x)) (term int))

(test-equal (term (lookup ((x int) (x (int -> int)) (y int)) y)) (term int)))

(define-metafunction TLambda-tc

lookup : any x -> any or #f

[(lookup ((x_1 any_1) ... (x any_t) (x_2 any_2) ...) x)

any_t

(side-condition (not (member (term x) (term (x_1 ...)))))]

[(lookup any_1 any_2)

#f])

2.16 "extend-lookup.rkt"

#lang racket

(provide

;; (extend σ (x ...) (v ...)) adds (x v) ... to σ

extend

;; (lookup σ x) retrieves x's value from σ

lookup)

;; ------------------------------------------------------------------

(require redex "common.rkt")

(define-metafunction Lambda

extend : ((x any) ...) (x ...) (any ...) -> ((x any) ...)

[(extend ((x any) ...) (x_1 ...) (any_1 ...))

((x_1 any_1) ... (x any) ...)])

(define-metafunction Lambda

lookup : ((x any) ...) x -> any or #f

[(lookup ((x_1 any_1) ... (x any_t) (x_2 any_2) ...) x)

any_t

(side-condition (not (member (term x) (term (x_1 ...)))))]

[(lookup any_1 any_2)

#f])

1	Amb: A Redex Tutorial
2	Long Tutorial
3	Extended Exercises
4	The Redex Reference
5	Automated Testing Benchmark
	Bibliography
	Index

2.1	The Theoretical Framework
2.2	Syntax and Metafunctions
2.3	Lab Designing Metafunctions
2.4	Reductions and Semantics
2.5	Lab Designing Reductions
2.6	Types and Property Testing
2.7	Lab Type Checking
2.8	Imperative Extensions
2.9	Lab Contexts and Stores
2.10	Abstract Machines
2.11	Lab Machine Transitions
2.12	Abstracting Abstract Machines
2.13	"common.rkt"
2.14	"close.rkt"
2.15	"tc-common.rkt"
2.16	"extend-lookup.rkt"

notation		meaning
x		basic notion of reduction, without properties
-->x		one-step reduction, generated from x, compatible with syntactic constructions
-->>x		reduction, generated from -->x, transitive here also reflexive
=x		“calculus”, generated from -->x, symmetric, transitive, reflexive